题目内容

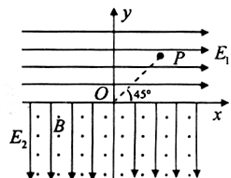
如图所示，直线PO与轴成角，轴上方有水平向右的匀强电场，下方有竖直向下的匀强电场，已知电场强度N/C，轴下方还有垂直纸面向外的匀强磁场，磁场的磁感应强度B=10T。现有一质量的带负电微粒，电荷量。微粒由P点无初速度释放，PO间距离（取），求：

   （1）微粒刚进入磁场区域时的速度的大小

   （2）微粒第一次在磁场中运动的时间和位移L

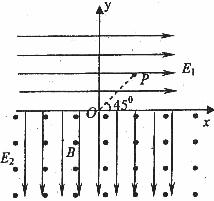
（1）微粒在两个电场中所受到的电场力大小相同，为：

微粒所受到的得力为：G=mg=1.0×10－4N

可见在两个电场中微粒受到的电场力大小均等于重力大小.

在x轴上方的电场中，微粒沿PO做初速度为0的匀加速直线运动，

合外力大小为：，方向与y轴负方向成45°角

则微粒将从O点进入x轴下方的复合场中. 加速度

微粒进入下方复合场的速度为：

（2）在x轴下方的复合场中，中于重力等于电场力，故微粒做匀速圆周运动

周期                                                                  

由对称性可知，微粒在磁场中运动了3/4周期，所用时间

半径                                                                       

微粒离开磁场时速度方向与x轴成45°，

则运动的位移为：

练习册系列答案
相关题目
（2009?茂名二模）如图所示，位于竖直平面内的坐标系xoy，在其第三象限空间有沿水平方向的、垂直于纸面向外的匀强磁场，磁感应强度大小为B，还有沿x轴负方向的匀强电场，场强大小为E．在其第一象限空间有沿y轴负方向的、场强为E′=
43
E的匀强电场，并在y＞h区域有磁感应强度也为B的垂直于纸面向里的匀强磁场．一个带电荷量为q的油滴从图中第三象限的P点得到一初速度，恰好能沿PO作直线运动（PO与x轴负方向的夹角为θ=37°），并从原点O进入第一象限．已知重力加速度为g，sin37°=0.6，cos37°=0.8，问：
（1）油滴的电性； 
（2）油滴在P点得到的初速度大小；
（3）油滴在第一象限运动的时间和离开第一象限处的坐标值．
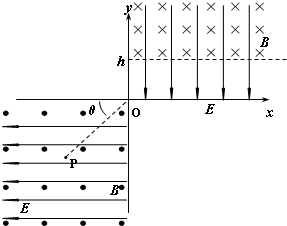如图所示，位于竖直平面内的坐标系xoy，在其第三象限空间有沿水平方向的、垂直于纸面向外的匀强磁场，磁感应强度大小为B=0.5T，还有沿x轴负方向的匀强电场，场强大小为E=
2NC
．在其第一象限空间有沿y轴负方向的、场强大小也为E的匀强电场，并在y＞h=0.4m的区域有磁感应强度也为B的垂直于纸面向里的匀强磁场．一个带电荷量为q的油滴从图中第三象限的P点得到一初速度，恰好能沿PO作匀速直线运动（PO与x轴负方向的夹角为θ=45°），并从原点O进入第一象限．已知重力加速度g=10m/s2，问：
（1）油滴在第一象限运动时受到的重力、电场力、洛伦兹力三力的大小之比；
（2）油滴在P点得到的初速度大小；
（3）油滴在第一象限运动的时间以及油滴离开第一象限处的坐标值．
如图所示，直线PO与x轴成45°角，x轴上方又水平向右的匀强电场E1，下方有竖直向下的匀强电场E2，已知电场强度E1=E2=l0N/C，x轴下方还存在着垂直纸面向外的匀强磁场，磁场的磁感应强度B=l0T．现有一质量m=1.0×10-5kg的带电粒子，带电荷量q=-1.0×10-5C．粒子由P点无初速释放，PO=d=
10
2
m （重力加速度g=10m/s2）．求：
（1）粒子刚进入磁场区域时的速度v
（2）粒子第一次在磁场中运动的时间t和位移L．

（10分）如图所示，直线PO与x轴成45°角，x轴上方又水平向右的匀强电场E1，下方有竖直向下的匀强电场E2,已知电场强度E1=E2=l0N/C，x轴下方还存在着垂直纸面向外的匀强磁场,磁场的磁感应强度B=l0T。现有一质量m=1.0×10-5kg的带电粒子,带电荷量q=-1.0×10-5C.粒子由P点无初速释放,PO=d=m(重力加速度g=10m/s2).求:

(1)粒子刚进入磁场区域时的速度v；

(2)粒子第一次在磁场中运动的时间t和位移L。

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网