��Ŀ����
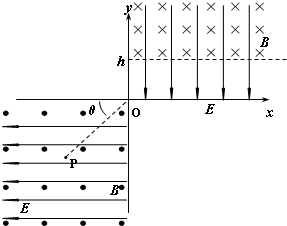 ��ͼ��ʾ��λ����ֱƽ���ڵ�����ϵxoy������������ռ�����ˮƽ����ġ���ֱ��ֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB=0.5T��������x�Ḻ�������ǿ�糡����ǿ��СΪE=
��ͼ��ʾ��λ����ֱƽ���ڵ�����ϵxoy������������ռ�����ˮƽ����ġ���ֱ��ֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB=0.5T��������x�Ḻ�������ǿ�糡����ǿ��СΪE=| 2N | C |
��1���͵��ڵ�һ�����˶�ʱ�ܵ����������糡�����������������Ĵ�С֮�ȣ�
��2���͵���P��õ��ij��ٶȴ�С��
��3���͵��ڵ�һ�����˶���ʱ���Լ��͵��뿪��һ����������ֵ��
��������1���͵��ڸ��ϳ�����ֱ���˶�����ֱ�ٶȷ���ĺ���һ��Ϊ�㣬����������ͼ��ʾ������͵δ����磬���������磨1����ʾ�������磬���������磨2����ʾ��

��ΪҪ��֤��ֱ�ٶȷ������Ϊ�㣬��2�����͵�һ���������˶�����ʱ���������ڱ仯�����´�ֱ�ٶȷ�����������仯���͵β�������ֱ���˶������͵β�����ֱ�ٶȷ������Ϊ�㣬���ٶȷ������ҲΪ�㣬��ֻ���ǣ�1��ͼ�������͵�һ�������磮
��2�����ݵ�һ�ʽ������������������ʽ��⣻
��3�����ӽ����һ����ʱ�������͵糡��ƽ�⣬��������������ֱ���˶�����������Բ���˶������������ֱ���˶������ݼ��ι�ϵ�����������ṩ������������ʱ�䲢ȷ���뿪��һ����λ�ã�

��ΪҪ��֤��ֱ�ٶȷ������Ϊ�㣬��2�����͵�һ���������˶�����ʱ���������ڱ仯�����´�ֱ�ٶȷ�����������仯���͵β�������ֱ���˶������͵β�����ֱ�ٶȷ������Ϊ�㣬���ٶȷ������ҲΪ�㣬��ֻ���ǣ�1��ͼ�������͵�һ�������磮
��2�����ݵ�һ�ʽ������������������ʽ��⣻
��3�����ӽ����һ����ʱ�������͵糡��ƽ�⣬��������������ֱ���˶�����������Բ���˶������������ֱ���˶������ݼ��ι�ϵ�����������ṩ������������ʱ�䲢ȷ���뿪��һ����λ�ã�
����⣺��1���͵δ�����ɣ����͵�����Ϊm��������ͼ

��ƽ��������ϼ��ι�ϵ�õ���
mg��qE��f=1��1��
��2����������������ʽ����
f=qvB
��
mg��qE��qvB=1��1��
��
v=
=4
m/s
��3�������һ���ޣ��糡����������ȣ�֪�͵���������ֱ���˶�������y��h�������������Բ���˶���·����ͼ������x���ϵ�N���뿪��һ���ޣ�
��O��A�����˶�λ��ΪS1=
=
h֪�˶�ʱ�䣺tt1=
=
=
=0.1s
�ɼ��ι�ϵ��Բ���˶������ڹ�ϵT=
֪��A��C��Բ���˶�ʱ��Ϊt2=
T=
���ɶԳ���֪��C��N��ʱ��t1=t3
�ڵ�һ�����˶�����ʱ�� t=t1+t2+t3=
+
=0.82s
���ڴų��е�����Բ���˶����С�qvB=m
����ù���뾶R=
=
ͼ�е�ON=2��S1cos45��+Rcos45�㣩=2(h+
)=4.0m
���͵��ڵ�һ�����˶���ʱ��Ϊ0.82s���뿪��һ������N�㣩������Ϊ��4.0m��0����

��ƽ��������ϼ��ι�ϵ�õ���
mg��qE��f=1��1��
| 2 |
��2����������������ʽ����
f=qvB
��
mg��qE��qvB=1��1��
| 2 |
��
v=
| ||
| B |
| 2 |
��3�������һ���ޣ��糡����������ȣ�֪�͵���������ֱ���˶�������y��h�������������Բ���˶���·����ͼ������x���ϵ�N���뿪��һ���ޣ�
��O��A�����˶�λ��ΪS1=
| h |
| sin45�� |
| 2 |
| S1 |
| v |
| ||||
|
| Bh |
| E |
�ɼ��ι�ϵ��Բ���˶������ڹ�ϵT=
| 2��m |
| qB |
| 1 |
| 4 |
| ��m |
| 2qB |
�ڵ�һ�����˶�����ʱ�� t=t1+t2+t3=
| 2Bh |
| E |
| ��E |
| 2qB |
���ڴų��е�����Բ���˶����С�qvB=m
| v2 |
| R |
| mv |
| qB |
| ||
| qB2 |
ͼ�е�ON=2��S1cos45��+Rcos45�㣩=2(h+
| E2 |
| qB2 |
���͵��ڵ�һ�����˶���ʱ��Ϊ0.82s���뿪��һ������N�㣩������Ϊ��4.0m��0����
����������ؼ�����ȷ��������˶�������������˶��켣��Ȼ�������η����������˶�������ƽ�⣬����Բ���˶������������ṩ��������

��ϰ��ϵ�д�
 ��ѧ����ϵ�д�
��ѧ����ϵ�д�
�����Ŀ
 ��ͼ��ʾ��λ����ֱƽ���ϵ�1/4Բ���⻬������뾶ΪR��OB����ֱ����Բ������϶�A������߶�ΪH������Ϊm��С���A�㾲ֹ�ͷţ����B��ˮƽ�ٶȴ�С��������O�������ͷ���B���ٶȴ�С����������ڵ���C�������ƿ����������� g=10m/s2����
��ͼ��ʾ��λ����ֱƽ���ϵ�1/4Բ���⻬������뾶ΪR��OB����ֱ����Բ������϶�A������߶�ΪH������Ϊm��С���A�㾲ֹ�ͷţ����B��ˮƽ�ٶȴ�С��������O�������ͷ���B���ٶȴ�С����������ڵ���C�������ƿ����������� g=10m/s2���� ��ͼ��ʾ��λ����ֱƽ���ϵ�
��ͼ��ʾ��λ����ֱƽ���ϵ� ��ͼ��ʾ��λ����ֱƽ���ϵ�
��ͼ��ʾ��λ����ֱƽ���ϵ�