题目内容
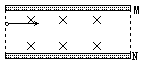
如图所示，MN为正对的两个平行板，可以吸附打到板上的电子，两板间距离为d，板长为7d．在两个平行板间只有方向垂直于纸面向里的匀强磁场．若有电量为e的电子流，从左侧不同位置进入两板间的虚线框区域，已知电子的动量大小为p，方向平行于板．为了使进入两板间的电子都能打到两板上，被两板吸收，磁场的磁感应强度大小取值可能是下述四个值中的①B=
| P |
| de |
| 3P |
| de |
| P |
| 20de |
| P |
| 25de |
分析：电子在进入磁场后，受到洛伦兹力作用下，做匀速圆周运动，根据题意可知，电子可能从左边射出磁场，也可能从右边射出磁场，因此结合几何关系，由牛顿第二定律，洛伦兹力提供向心力，得出运动的轨迹的半径公式，即可求解．
解答：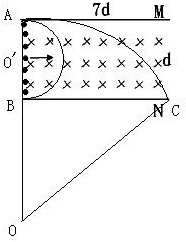
解：洛伦兹力提供向心力，由牛顿第二定律，可得，Bqv=m
，
则有R=
①，
根据题意，结合几何关系，由图可知，AB=d，因此R=
②，
或者OC2=BC2+BO2，而BC=7d，BO=R-d，
因此解得，R=25d③，
所以由①②③可得，B=
=
，
或者B=
，故B正确，ACD错误；
故选：B．
解：洛伦兹力提供向心力，由牛顿第二定律，可得，Bqv=m| v2 |
| r |
则有R=
| mv |
| Bq |
根据题意，结合几何关系，由图可知，AB=d，因此R=
| d |
| 2 |
或者OC2=BC2+BO2，而BC=7d，BO=R-d，
因此解得，R=25d③，
所以由①②③可得，B=
| 2mv |
| de |
| 2P |
| de |
或者B=
| P |
| 25de |
故选：B．
点评：考查粒子在磁场中受到洛伦兹力作用下，做匀速圆周运动，掌握牛顿第二定律的应用，理解向心力表达式，注意几何关系的运用．
练习册系列答案
相关题目
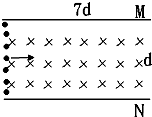如图所示，MN为正对的两个平行板，可以吸附打到板上的电子，两板间距距离为d，板长为7d在两个平行板间只有方向垂直于纸面向里的匀强磁场．若有电量为e的电子流，从左侧不同位置进入两板间的虚线框中，已知电子的动量大小为p，方向平行于板．为了使进入两板间的电子都能打到两板上，被两板接收，磁场的磁感应强度大小取值可能是下述四个值中的（ ）
②B＝
③B＝
④B＝
B．
D．
