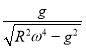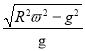题目内容
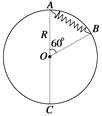
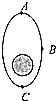
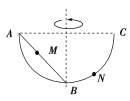
【题目】如图所示,处于竖直平面内的光滑细金属圆环半径为R,质量均为m的带孔小球A、B穿于环上,两根长为R的细绳一端分别系于A、B球上,另一端分别系于圆环的最高点和最低点,现让圆环绕竖直直径转动,当角速度缓慢增大到某一值时,连接B球的绳子恰好拉直,转动过程中绳不会断,则下列说法正确的是( )
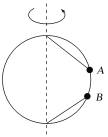
A. 连接B球的绳子恰好拉直时,转动的角速度为![]()
B. 连接B球的绳子恰好拉直时,金属圆环对A球的作用力为零
C. 继续增大转动的角速度,金属环对B球的作用力可能为零
D. 继续增大转动的角速度,A球可能会沿金属环向上移动
【答案】AB
【解析】
球A、B均做匀速圆周运动,合力提供向心力,考虑细线拉力为零的临界情况,根据牛顿第二定律列式分析即可.
A、当连接B球的绳刚好拉直时,mgtan60°=mω2Rsin60°,求得![]() ,A项正确;
,A项正确;
B、连接B球的绳子恰好拉直时,A球与B球转速相同,A球所受合力也为mgtan60°,又小球A所受重力为mg,可判断出A球所受绳的拉力为2mg,A球不受金属圆环的作用力,B项正确;
C、继续增大转动的角速度,连接B球的绳上会有拉力,要维持B球竖直方向所受外力的合力为零,环对B球必定有弹力,C项错误;
D、当转动的角速度增大,环对B球的弹力不为零,根据竖直方向上A球和B球所受外力的合力都为零,可知绳对A球的拉力增大,绳应张得更紧,因此A球不可能沿环向上移动,D项错误.
故选AB.

练习册系列答案
相关题目