Question

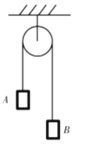
【题目】如图所示，完全相同的两个弹性环A、B用不可伸长的、长为L的轻绳连接，分别套在水平细杆OM和竖直细杆ON上，OM与ON在O点用一小段圆弧杆平滑相连（圆弧长度可忽略），且ON足够长。初始时刻，将轻绳拉至水平位置伸直，然后静止释放两个环，此后某时刻，A环通过O点小段圆弧杆速度大小保持不变，重力加速度为g，不计一切摩擦，试求：

(1)当B环下落至轻绳与竖直方向夹角θ=60°时，A环的速度大小；

(2)若两环碰撞时间极短，A环和B环第一次碰撞后瞬间的速度大小分别为多少？

Answer 1

【答案】(1)；(2)，

【解析】

(1)B环下落至轻绳与竖直方向夹角，即B环下降，此时轻绳与水平方向之间的夹角满足，设A、B两环速度分别为、，则

即

设A环、B环质量均为m，B环下降的过程中，A与B组成的系统机械能守恒

所以A环的速度

(2)设A环到达O点时速度为，此时B环的速度等于0，B环下降L过程中，由于A、B系统机械能守恒

即

环A过O点后做初速度为，加速度为g的匀加速直线运动，环B做自由落体运动；

设从A环经过O点开始，追上B环用时，A、B即将发生第一次碰撞时二者的速度分别为v1、v2，则有

即

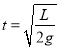
故A环追上B环时

A、B发生弹性碰撞，设第一次碰撞后瞬间A、B速度分为、，

根据动量守恒定律，有

根据机械能守恒定律，有

解得