题目内容
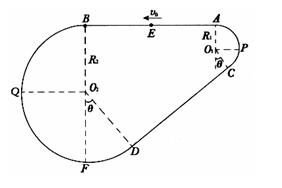
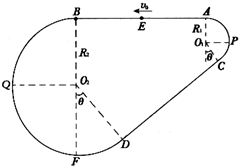 如图是放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的 金属杆组成:水平直轨AB,半径分别为R1=1.0m和R2=3.0m的弧形轨道APC和BQD,倾斜直轨 CD长为L=6m,AB、CD与两圆形轨道相切,其中倾斜直轨CD部分表面粗糙,动摩 擦因数为μ=
如图是放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的 金属杆组成:水平直轨AB,半径分别为R1=1.0m和R2=3.0m的弧形轨道APC和BQD,倾斜直轨 CD长为L=6m,AB、CD与两圆形轨道相切,其中倾斜直轨CD部分表面粗糙,动摩 擦因数为μ=| 1 | 6 |
求:( 1)滑环第一次通过圆O2的最低点F处时对轨道的压力;
(2)滑环在克服摩擦力做功过程中所经过的总路程.
分析:(1)滑环第一次由E到F点过程由机械能守恒定律求解速度.根据牛顿第二定律和第三定律求出最低点F处时对轨道的压力.
(2)滑环在每次经过 DC段时克服摩擦力做功,机械能转化为内能,所以由功能关系求解.其中路程包含在摩擦力做功里.
(2)滑环在每次经过 DC段时克服摩擦力做功,机械能转化为内能,所以由功能关系求解.其中路程包含在摩擦力做功里.
解答:解:(1)滑环第一次由E到F点过程由机械能守恒定律:
+mg?2R2=
①
在F点,满足:FN-mg=
②
由①②解得:FN=166.7N
由牛顿第三定律知,滑环对轨道压力高为166.7N
(2)滑环在每次经过 DC段时克服摩擦力做功,机械能转化为内能,最终滑环在圆O2底部做往复运动,到D点时动能为0.
设滑环克服摩擦力做功经过的路程为S,则由功能关系得:
+mgR2(1+cosθ)=μmgScosθ
解得S=78cm
答:( 1)滑环第一次通过圆O2的最低点F处时对轨道的压力是166.7N;
(2)滑环在克服摩擦力做功过程中所经过的总路程是78cm.
| 1 |
| 2 |
| mv | 2 0 |
| 1 |
| 2 |
| mv | 2 F |
在F点,满足:FN-mg=
| ||
| R2 |
由①②解得:FN=166.7N
由牛顿第三定律知,滑环对轨道压力高为166.7N
(2)滑环在每次经过 DC段时克服摩擦力做功,机械能转化为内能,最终滑环在圆O2底部做往复运动,到D点时动能为0.
设滑环克服摩擦力做功经过的路程为S,则由功能关系得:
| 1 |
| 2 |
| mv | 2 0 |
解得S=78cm
答:( 1)滑环第一次通过圆O2的最低点F处时对轨道的压力是166.7N;
(2)滑环在克服摩擦力做功过程中所经过的总路程是78cm.
点评:了解研究对象的运动过程是解决问题的前提,根据题目已知条件和求解的物理量选择物理规律解决问题.
运用动能定理时,容易出错的地方是功的求解,对于多过程我们要分开求解.
运用动能定理时,容易出错的地方是功的求解,对于多过程我们要分开求解.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案
相关题目
 如图是放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成,水平直轨AB,半径分别为R1=1.0m和R2=3.0m的弧形轨道,倾斜直轨CD长为L=6m且表面粗糙,动摩擦因数为
如图是放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成,水平直轨AB,半径分别为R1=1.0m和R2=3.0m的弧形轨道,倾斜直轨CD长为L=6m且表面粗糙,动摩擦因数为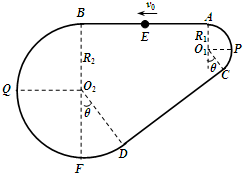 如图是放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成:光滑水平直轨AB,半径分别为R1=1.0m和R2=3.0m的光滑弧形轨道,倾斜直轨CD长为L=6m,AB、CD与两圆形轨道相切.有质量为m=2kg的小球穿在滑轨上,小球与CD杆间的动摩擦因数为μ=
如图是放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成:光滑水平直轨AB,半径分别为R1=1.0m和R2=3.0m的光滑弧形轨道,倾斜直轨CD长为L=6m,AB、CD与两圆形轨道相切.有质量为m=2kg的小球穿在滑轨上,小球与CD杆间的动摩擦因数为μ=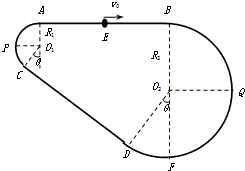 如图是放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成:水平直轨AB,半径分别为R1=1.0m和R2=3.0m的弧形轨道,倾斜直轨CD长为L=6m,AB、CD与两圆形轨道相切,其中倾斜直轨CD部分表面粗糙,动摩擦因数为μ=
如图是放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成:水平直轨AB,半径分别为R1=1.0m和R2=3.0m的弧形轨道,倾斜直轨CD长为L=6m,AB、CD与两圆形轨道相切,其中倾斜直轨CD部分表面粗糙,动摩擦因数为μ=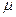 =
=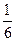 ,其余各部分表面光滑。一质量为m=2kg的滑环套在滑轨上,从AB的中点E处以V0=10m/s的初速度水平向左运动。已知
,其余各部分表面光滑。一质量为m=2kg的滑环套在滑轨上,从AB的中点E处以V0=10m/s的初速度水平向左运动。已知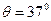 ,sin37°=0.6,cos37°=0.8(取g=10m/s2)
,sin37°=0.6,cos37°=0.8(取g=10m/s2)