题目内容
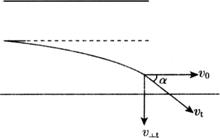
如图所示,由质子源(质子源的大小不计)放出的质子(质量为m,电量为e)从静止开始,被电压为U1的加速电场加速后,紧接着垂直于电场方向进入长度为L,板间距为D,两板间电压为U2的水平放置的平行板偏转电场中,并能全部穿过偏转电场.(1)试推导出质子流在偏转电场中的偏转角正切值的表达式.
(2)在加速电场中,若加速电压U1=800 kV,质子形成了电流强度I=1 mA粗细均匀的细柱形的质子流,已知e=1.6×10
(3)在(2)的条件下,选取在距离质子源l/4处的a点和加速电场的出口b点极小的一段质子流,则这两小段质子流中的质子数N1和N2的比值为多少?
解:(1)质子在加速电场中时U1e=![]() mV12 ①
mV12 ①
当它进入偏转电场中时E2=![]() ,电场力F=
,电场力F=![]()
由牛顿第二定律:a=![]() ②
②
质子在偏转场中做类平抛运动,水平方向匀速运动,它穿过此电场所用时间t=![]() ③
③
它在垂直于偏转板方向做初速为零的匀加速运动,射出时,此方向的末速度V⊥t=at ④
其偏转α的正切值为tanα=![]() ⑤
⑤
由①②③④⑤得
tanα=![]()

(2)设每秒通过细柱横截面的质子数为n
I=![]() =
=![]() n=
n=![]() =6.25×1015个
=6.25×1015个
(3)当质子从粒子源到a点时
![]() ,即va=
,即va=![]() ⑥
⑥
同理:vb=![]() ⑦
⑦
由于细柱各处电流相同,由I=nesv
N1esva=N2esvb
即![]() =
=![]() =
=![]()

练习册系列答案
相关题目
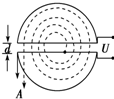 如图所示,回旋加速器D形盒的半径为R,所加磁场的磁感应强度为B,用来加速质量为m、电荷量为q的质子,质子从下半盒的质子源由静止出发,加速到最大能量E后,由A孔射出.则下列说法正确的是( )
如图所示,回旋加速器D形盒的半径为R,所加磁场的磁感应强度为B,用来加速质量为m、电荷量为q的质子,质子从下半盒的质子源由静止出发,加速到最大能量E后,由A孔射出.则下列说法正确的是( )| A、回旋加速器不能无限加速质子 | ||||
| B、增大交变电压U,则质子在加速器中运行时间将变短 | ||||
C、回旋加速器所加交变电压的频率为
| ||||
D、下半盒内部,质子的轨道半径之比(由内到外)为1:
|
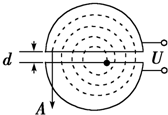 如图所示,回旋加速器D形盒的半径为R,所加磁场的磁感应强度为B,用来加速质量为m、电荷量为q的质子,质子从下半盒的质子源由静止出发,加速到最大动能E后由A孔射出,则下列说法正确的是( )
如图所示,回旋加速器D形盒的半径为R,所加磁场的磁感应强度为B,用来加速质量为m、电荷量为q的质子,质子从下半盒的质子源由静止出发,加速到最大动能E后由A孔射出,则下列说法正确的是( )| A、回旋加速器不能无限加速粒子 | ||||
| B、质子在加速器中运行时间与交变电压U大小无关 | ||||
C、回旋加速器所加交变电压的频率为
| ||||
D、下半盒内部质子的轨道半径之比(由内到外)为1:
|
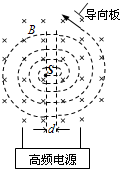 正电子发射计算机断层(PET)是分子水平上的人体功能显像的国际领先技术,它为临床诊断和治疗提供全新的手段.
正电子发射计算机断层(PET)是分子水平上的人体功能显像的国际领先技术,它为临床诊断和治疗提供全新的手段.