题目内容
 如图,质量为m的小物体沿
如图,质量为m的小物体沿| 1 |
| 4 |
分析:由重力做功只与初末位置高度差有关,可求得重力的功,由于摩擦力是变力,故要由动能定理来求它的功,由动能定理还可以得到合理的功
解答:解:
A、重力做功等于重力乘以初末位置高度差,故此过程重力的功为:mgR,故A正确
BCD、由动能定理:mgR+Wf=
mv2-0,解得:Wf=
mv2-mgR,故克服摩擦力做功为:mgR-
mv2,故B错误,C正确,合外力做的功等于动能变化W=
mv2-0,故D正确
故选:ACD.
A、重力做功等于重力乘以初末位置高度差,故此过程重力的功为:mgR,故A正确
BCD、由动能定理:mgR+Wf=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选:ACD.
点评:解决本题关键要注意机械能是不守恒的,不要用机械能守恒来做,其次要掌握好重力做功的特征.

练习册系列答案
相关题目
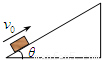
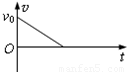
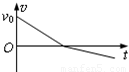
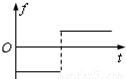
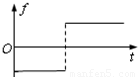
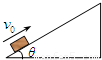
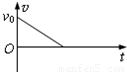
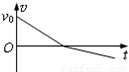
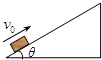 (2011?江苏模拟)如图:质量为m的小物块以初速度v0沿足够长的固定斜面上滑,斜面倾角为θ,物块与该斜面间的动摩擦因数μ>tanθ,图中表示该物块的速度v和所受摩擦力f随时间t变化的图线(以初速度v0的方向为正方向),可能正确的是( )
(2011?江苏模拟)如图:质量为m的小物块以初速度v0沿足够长的固定斜面上滑,斜面倾角为θ,物块与该斜面间的动摩擦因数μ>tanθ,图中表示该物块的速度v和所受摩擦力f随时间t变化的图线(以初速度v0的方向为正方向),可能正确的是( )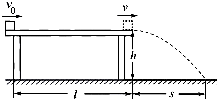 如图,质量为m的小物块在粗糙水平桌面上做直线运动,经距离l后以速度v飞离桌面,最终落在水平地面上.已知l=1.4m,s=0.90m,m=0.10kg,物块与桌面间的动摩擦因数μ=0.25,桌面高h=0.45m.不计空气阻力,重力加速度g取10m/s2.求
如图,质量为m的小物块在粗糙水平桌面上做直线运动,经距离l后以速度v飞离桌面,最终落在水平地面上.已知l=1.4m,s=0.90m,m=0.10kg,物块与桌面间的动摩擦因数μ=0.25,桌面高h=0.45m.不计空气阻力,重力加速度g取10m/s2.求