题目内容
 一个重量为G=100N的物体,放在固定的粗糙斜面上,斜面与水平方向的夹角为37°,物体与斜面间的动摩擦因素μ=0.5,可以近似认为物体所受到的最大静摩擦力等于滑动摩擦力,现在用一个水平向右的推力F作用在物体上,求:
一个重量为G=100N的物体,放在固定的粗糙斜面上,斜面与水平方向的夹角为37°,物体与斜面间的动摩擦因素μ=0.5,可以近似认为物体所受到的最大静摩擦力等于滑动摩擦力,现在用一个水平向右的推力F作用在物体上,求:(1)若力F使物体沿斜面匀速向上运动,则F为多大?(sin37°=0.6,cos37°=0.8)
(2)推力F的大小在什么范围内,可以使物体在斜面上保持静止?
分析:物体做匀速运动或静止时,物体受力平衡,对物体受力分析应用平衡条件列式求解.
解答:解:对物体受力分析并分解如图:

由平衡条件得:Fmaxcosθ=mgsinθ+f;
N=mgcosθ+Fmaxsinθ
又:f=μN
即:Fmaxcosθ-mgsinθ=μ(mgcosθ+Fmaxsinθ)代入数据得:
0.8Fmax-10×10×0.6=0.5×(10×10×0.8+0.6Fmax)
解得:Fmax=200N
(2)当物体在斜面上静止且所受摩擦力沿斜面向上时,推力F可有最小值.
由平衡条件得:Fmincosθ+f-mgsinθ=0;
N=mgcosθ+Fminsinθ
又:f=μN
故联立可解得:Fmin=
N
故物体在斜面上保持静止时,应满足:
N≤F≤200N
答:(1)若力F使物体沿斜面匀速向上运动,则F为200N
(2)推力F的大小满足:
N≤F≤200N时,可以使物体在斜面上保持静止.

由平衡条件得:Fmaxcosθ=mgsinθ+f;
N=mgcosθ+Fmaxsinθ
又:f=μN
即:Fmaxcosθ-mgsinθ=μ(mgcosθ+Fmaxsinθ)代入数据得:
0.8Fmax-10×10×0.6=0.5×(10×10×0.8+0.6Fmax)
解得:Fmax=200N
(2)当物体在斜面上静止且所受摩擦力沿斜面向上时,推力F可有最小值.
由平衡条件得:Fmincosθ+f-mgsinθ=0;
N=mgcosθ+Fminsinθ
又:f=μN
故联立可解得:Fmin=
| 200 |
| 11 |
故物体在斜面上保持静止时,应满足:
| 200 |
| 11 |
答:(1)若力F使物体沿斜面匀速向上运动,则F为200N
(2)推力F的大小满足:
| 200 |
| 11 |
点评:对物体进行受力分析,运用力的合成或分解结合共点力平衡条件解决问题.一般3个力用合成法,4个以上的力用正交分解法.

练习册系列答案
相关题目
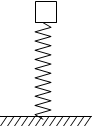 如图所示原长为L0=100cm的轻质弹簧竖直放在地面上,上端放上一个重量为G=10N的物体(物体与弹簧不拴接)静止时弹簧的长度为L1=80cm.现将该物体提高到离地面H=1.8m的高度从静止开始释放,不计空气阻力,测得物体从静止下落到沿竖直向下压缩弹簧达最低点所用的总时间为t=0.65s,弹簧对地面的最大作用力为Fm=40N,上述过程均在弹性限度内,g取10m/s2,求:
如图所示原长为L0=100cm的轻质弹簧竖直放在地面上,上端放上一个重量为G=10N的物体(物体与弹簧不拴接)静止时弹簧的长度为L1=80cm.现将该物体提高到离地面H=1.8m的高度从静止开始释放,不计空气阻力,测得物体从静止下落到沿竖直向下压缩弹簧达最低点所用的总时间为t=0.65s,弹簧对地面的最大作用力为Fm=40N,上述过程均在弹性限度内,g取10m/s2,求: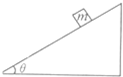 一个重量为G=100N的物体,放在固定的粗糙斜面上,斜面与水平方向的夹角为37°,物体静止不动,求:
一个重量为G=100N的物体,放在固定的粗糙斜面上,斜面与水平方向的夹角为37°,物体静止不动,求:
