Question

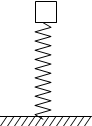如图所示原长为L₀=100cm的轻质弹簧竖直放在地面上，上端放上一个重量为G=10N的物体（物体与弹簧不拴接）静止时弹簧的长度为L₁=80cm．现将该物体提高到离地面H=1.8m的高度从静止开始释放，不计空气阻力，测得物体从静止下落到沿竖直向下压缩弹簧达最低点所用的总时间为t=0.65s，弹簧对地面的最大作用力为F_m=40N，上述过程均在弹性限度内，g取10m/s²，求：
（1）弹簧的劲度系数？
（2）物体自由下落所用的时间？
（3）物体压缩弹簧过程的平均速度？

Answer 1

分析：（1）根据共点力平衡求出弹簧的弹力，结合胡克定律求出弹簧的劲度系数．
（2）根据物体自由落体的高度，结合位移时间公式求出自由下落的时间．
（3）根据压缩弹簧的长度和时间，结合平均速度的定义式求出平均速度的大小．

解答：解：（1）根据共点力平衡得，G=k（L₀-L₁）
解得劲度系数k=

G

L0-L1

=

10

1-0.8

N/m=50N/m．
（2）物体自由下落的高度h=H-L₀=1.8-1m=0.8m．
根据h=

1

2

gt12得，t₁=

2h g

=

2×0.8 10

s=0.4s．
（3）物体压缩弹簧到最低点，弹簧的弹力为40N．
根据F_m=kx₂得，x2=

Fm

k

=

40

50

m=0.8m．
物体压缩弹簧的时间t₂=t-t₁=0.65-0.4s=0.25s．
物体压缩弹簧过程中的平均速度

.

v

=

x2

t2

=

0.8

0.25

m/s=3.2m/s．
答：（1）弹簧的劲度系数为50N/m．
（2）物体自由下落所用的时间为0.4s．
（3）物体压缩弹簧过程的平均速度为3.2m/s．

点评：本题考查了共点力平衡、胡克定律和运动学公式的基本运用，难度不大．知道物体与弹簧接触后不再是自由落体运动．