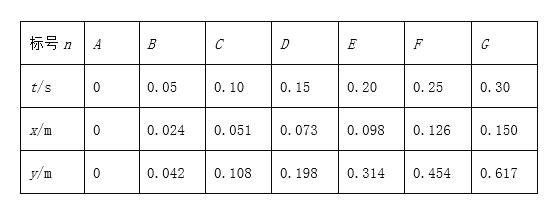
题目内容
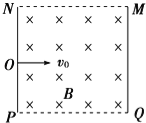
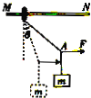
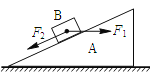
【题目】如图甲所示，一端带有定滑轮的长木板放在水平桌面上，靠近长木板的左端固定有一光电门，右端放置一带有细立柱的小车，小车和细立柱的总质量为M，细线绕过定滑轮，端与小车相连，另一端挂有5个钩码，已知每个钩码的质量为m，且M=5m。
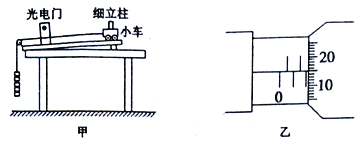
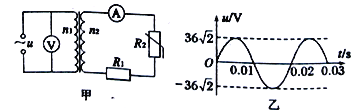
(1)用螺旋测微器测小车上的细立柱的直径时，结果如图乙所示，则螺旋测微器读数为___________mm。
(2)把木板右端适当垫高，调节木板的倾斜程度，使小车在不受细线的拉力时能沿木板做匀速直线运动。
(3)将小车从木板右端由静止释放，记录小车上的细立柱通过光电门的时间t。
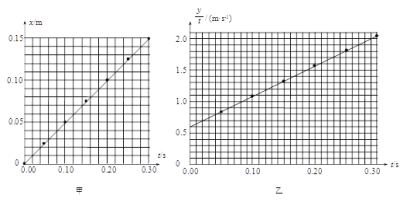
(4)开始实验时，细线另一端挂有5个钩码，然后每次实验时将1个钩码移到小车上，若每次移动钩码后都从同一位置释放小车，设细立柱宽度为d，释放小车时细立柱与光电门的距离为L，d<<L，细线所挂钩码的个数为n，每次细立柱通过光电门的时间为t，绘出
-n图象如图所示，已知图线斜率为k，则当地重力加速度为___________(用题中所给字母表示)
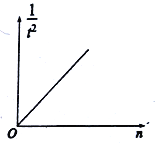
【答案】(1) 2.150(2.148～2.152均可） (4) g＝5kd2/L
【解析】
（1）根据螺旋测微器的读数规则分别读出固定尺加上螺旋尺刻度即可；（2）根据极短时间内的平均速度等于瞬时速度求出滑块通过光电门的速度。根据速度位移公式，结合牛顿第二定律得出n-
的表达式，结合图线的斜率求出当地的重力加速度．
(1)螺旋测微器的固定尺读数为2mm，螺旋尺读数为0.01×15.0mm=0.150mm，则最终读数为2mm+0.150mm=2.150mm.
(2)极短时间内的平均速度等于瞬时速度的大小，则细立柱通过光电门的速度v=d/t.
对整体分析，
根据v2=2aL得，
，得
所以k=
，当地重力加速度为g＝5kd2/L.
【题目】某同学通过实验探究小灯泡的伏安特性曲线。除了导线、开关和小灯泡之外，实验室提供的器材还有：
A．电流表（A1）：量程0—0.6A，内阻约0.125Ω
B．电流表（A2）：量程0—3A，内阻约0.025Ω
C．电压表（V1）：量程0—3V，内阻约3kΩ
D．电压表（V2）：量程0—15V，内阻约15kΩ
E．滑动变阻器（R1）：总阻值约10Ω
F．滑动变阻器（R2）：总阻值约200Ω
G．一组干电池，其电动势为3.0V，内阻很小
该同学选择仪器，设计电路并进行实验，通过实验得到如下数据：
U/V | 0 | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 | 1.20 | 1.40 | 1.60 | 1.80 | 2.00 |
I/A | 0 | 0.12 | 0.21 | 0.29 | 0.34 | 0.38 | 0.42 | 0.45 | 0.47 | 0.49 | 0.50 |
（1）请把该同学设计的实验电路图画在图甲的方框中___________________。
（2）在探究实验中该同学选择的器材是：电流表为_________，电压表为_________，滑动变阻器为___________（以上均填写器材代号）。
（3）请在图乙的坐标系中画出小灯泡的I—U图线________________。
（4）根据该实验的测量数据，得出的有关小灯泡电阻的结论是__________________；你对该实验结论的解释是________________________。
（5）用导线将该小灯泡直接连在某一电源的两极之间，要使小灯泡的实际发热功率约为0.27W。那么，电源的电动势和内电阻应该分别最接近_________________
A．1.5V、2.0Ω B．1.5V、0.5Ω
C.3.0V、0.5Ω D．3.0V、2.0Ω
