题目内容
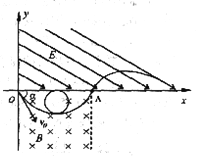
【题目】如图所示的坐标系中，第一象限内存在与x轴成300角斜向下的匀强电场，电场强度E=400N/C；第四象限内存在垂直于纸面向里的有界匀强磁场，x轴方向的宽度OA=20
cm，轴负方向无限大，磁感应强度B=1×10-4T．现有一比荷为
=2×1011C/kg的正离子(不计重力)，以某一速度v0从O点射入磁场，α=600，离子通过磁场后刚好从A点射出，之后进入电场．
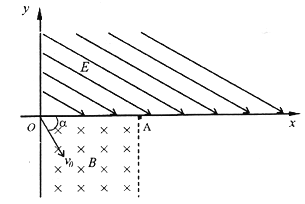
(1)求离子进入磁场B的速度v0的大小；
(2)离子进入电场后，经多少时间再次到达x轴上；
(3)若离子进入磁场B后，某时刻再加一个同方向的匀强磁场使离子做完整的圆周运动，求所加磁场磁感应强度的最小值．
【答案】（1）4×106 m/s （2）
（3）
【解析】试题分析：(1)如图所示，由几何关系得离子在磁场中时的轨道半径r1=0.2m
离子在磁场中做匀速圆周运动，洛伦兹力提供向心力
解得：v0=4×106m/s
(2)离子进入磁场后，设经过实践t再次到达x轴上，离子沿垂直电场方向做速度为v0的匀速直线运动，位移为l1，则l1=v0t
离子沿电场方向做初速度为零的匀加速直线运动，加速度为a，位移为l2
Eq=ma
由几何关系可知： 
代入数据解得： 
（3）由
知，B越小，r越大，设粒子在磁场中最大半径为R
由几何关系得： 
由牛顿运动定律得： 
得： 
则外加磁场
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
