题目内容
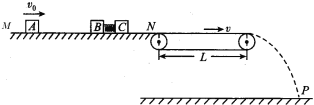
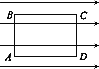
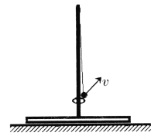
【题目】一玩具厂家设计了一款玩具,模型如下。游戏时玩家把压缩的弹簧释放后使得质量m=0.2kg的小弹丸A获得动能,弹丸A再经过半径R0=0.1m的光滑半圆轨道后水平进入光滑水平平台,与静止的相同的小弹丸B发生碰撞,并在粘性物质作用下合为一体。然后从平台O点水平抛出,落于水平地面上设定的得分区域。已知压缩弹簧的弹性势能范围为![]() J,距离抛出点正下方O点右方0.4m处的M点为得分最大值处,小弹丸均看作质点。
J,距离抛出点正下方O点右方0.4m处的M点为得分最大值处,小弹丸均看作质点。
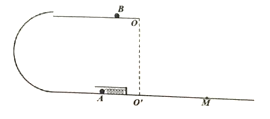
(1)要使得分最大,玩家释放弹簧时的弹性势能应为多少?
(2)得分最大时,小弹丸A经过圆弧最高点时对圆轨道的压力大小。
(3)若半圆轨道半径R可调(平台高度随之调节)弹簧的弹性势能范围为![]() J,玩家要使得落地点离O点最远,则半径应调为多少?最远距离多大?
J,玩家要使得落地点离O点最远,则半径应调为多少?最远距离多大?
【答案】(1)2J (2) 30N (3) 0.5m,1m
【解析】
(1)根据机械能守恒定律得:
![]()
A、B发生碰撞的过程,取向右为正方向,由动量守恒定律有:
mv1=2mv2
![]()
x=v2t0
解得:
Ep=2J
(2)小弹丸A经过圆弧最高点时,由牛顿第二定律得:
![]()
解得:
FN=30N
由牛顿第三定律知:
F压=FN=30N
(3)根据
![]()
mv1=2mv2
2R=![]() gt2,
gt2,
x=v2t
联立解得:
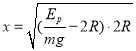
其中Ep最大为4J,得 R=0.5m时落点离O′点最远,为:
xm=1m

 期末1卷素质教育评估卷系列答案
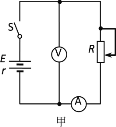
期末1卷素质教育评估卷系列答案【题目】某同学用图甲所示电路测一电池组(两节新干电池)的总电动势和总内电阻,除了电池组、电键S和导线,实验室还提供如下实验器材:
次数 | 1 | 2 | 3 | 4 | 5 | 6 |
I/A | 0.100 | 0.200 | 0.300 | 0.400 | 0.500 | 0.600 |
U/V | 3.00 | 2.97 | 2.95 | 2.92 | 2.89 | 2.87 |
A.电压表(量程0 - 3 V,内阻约为3 kΩ)
B.电压表(量程0 - 15 V,内阻约为15 kΩ)
C.电流表(量程0 - 0.6 A,内阻约为0.17 Ω)
D.电流表(量程0 - 3 A,内阻约为0.03 Ω)
E.滑动变阻器(阻值范围0~10 Ω,额定电流2 A)
F.滑动变阻器(阻值范围0~50 Ω,额定电流1 A)
(1)该同学选取了恰当的实验器材,接好电路并正确操作,测出6组数据填入上面表格中.由表格中数据可知实验中用的电压表是_______,电流表是_______,滑动变组器是_______.(填字母符号)
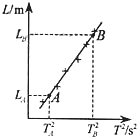
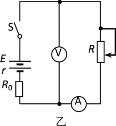
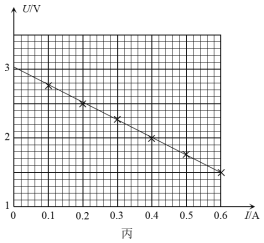
(2)该同学改用图乙所示的电路,重做一次实验,并由实验数据画出图丙所示的U - I图象.已知R0=2.30 Ω,由图象可求得该电池组的电动势为_________V,内阻为_________Ω.
(3)定值电阻R0的主要作用是_________
A.保护电池组,无论如何调节R,电流都不超过3 A
B.保护电流表,无论如何调节R,电流都不超过量程
C.保护滑动变阻器,无论如何调节R都不超额定电流
D.相当于增大电池组的内阻,使端电压改变量增大,方便实验数据的读取和处理