题目内容
关于万有引力定律,下列说法中正确的是 ( ).
| A.G值的测出使万有引力定律有了真正的实用价值,是牛顿测出。 |
B.由F= 可知,两物体间距离r减小时,它们之间的引力增大,距离r趋于零时,万有引力无限大 可知,两物体间距离r减小时,它们之间的引力增大,距离r趋于零时,万有引力无限大 |
| C.引力常量G的物理意义是:两个质量都是1 kg的质点相距1 m时相互吸引力为6.67×10-11 N |
| D.引力常量G值大小与中心天体选择有关 |
C
试题分析:万有引力定律是由牛顿发现的,而万有引力恒量是由卡文迪许测定的.万有引力定律适用于质点间的相互作用.G是一个比例常量,但有单位.
A、卡文迪许用扭秤实验证明万有引力定律是正确的,并测出万有引力恒量,故A错误;
B、万有引力定律适用于质点间的相互作用的计算.故BD错误.
C、G是一个比例常量,但有单位,单位是N?m2/kg2,引力常量G的物理意义是:两个质量都是1 kg的质点相距1 m时相互吸引力为6.67×10-11 N.故C正确;
故选C.
点评:对于物理学上重要实验、发现和理论,要加强记忆,这也是高考考查内容之一.从公式的适用条件、物理意义、各量的单位等等全面理解万有引力定律公式.

练习册系列答案
相关题目
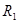 ,周期为
,周期为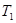 。已知万有引力常量为G。
。已知万有引力常量为G。 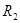 ,周期为
,周期为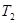 ,试估算该行星周围众多卫星的总质量。
,试估算该行星周围众多卫星的总质量。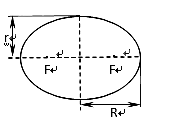
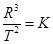 ,常量K与行星无关
,常量K与行星无关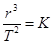 ,常量K与行星无关
,常量K与行星无关

