题目内容
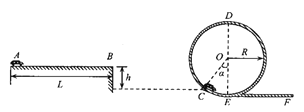
【题目】如图所示,在竖直平面内有一个四分之一圆弧轨道固定在水平桌面上,圆心为O点,OA在水平方向,其半径R=0.40 m ,轨道的最低点B距地面的高度h=0.45 m。一质量m=0.20kg的小滑块从轨道的最高点A由静止开始滑下,到达轨道底端B点的速度vB = 2.0m/s。滑块离开轨道后做平抛运动,落到地上的C点。不计空气阻力,重力加速度g=10m/s2。求:
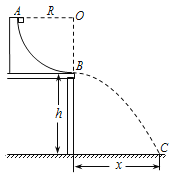
(1)小滑块从B点运动到C点所经历的时间t;
(2)小滑块落地点与B点的水平距离x;
(3)小滑块从A点运动到B点的过程中,滑块克服摩擦力所做的功W。
【答案】(1)0.30s(2)0.60m(3)0.40J
【解析】以小滑块为研究对象
(1)从B到C,根据平抛运动规律,竖直方向![]() ,代入数据解得
,代入数据解得![]()
(2)水平方向![]() ,代入数据解得
,代入数据解得![]()
(3)从A到B,根据动能定理![]() ,代入数据解得W = 0.40J
,代入数据解得W = 0.40J

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某同学测一节干电池的电动势和内电阻,现提供器材如下:
A.电压表V:(0~3V和0~15V两个量程) |
B.电流表A:(0~0.6A和0~3A两个量程) |
C.滑动变阻器R1(最大阻值20Ω) |
D.滑动变阻器R2(最大阻值100Ω) |
E.开关S和导线若干
(1)电流表应选用 量程;电压表应选用 量程;滑动变阻器应选 (选填R1或R2)
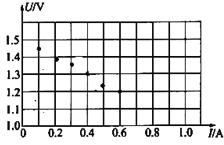
(2)根据实验中所测的六组数据标在图示的U﹣I图中,请根据图像,求出E= V,r= Ω.