题目内容
4.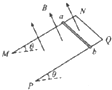 如图,足够长的U型光滑金属导轨平面与水平面成θ角(0<θ<90°),其中MN和PQ平行且间距为L,导轨平面与磁感应强度为B的匀强磁场垂直,导轨电阻不计.金属棒ab棒质量为m,接入电路的电阻为R,并与两导轨始终保持垂直且良好接触,使棒ab由静止开始沿导轨下滑,当流过ab棒某一横截面的电量为q时,它的速度大小为v,则金属棒ab在这一过程中( )
如图,足够长的U型光滑金属导轨平面与水平面成θ角(0<θ<90°),其中MN和PQ平行且间距为L,导轨平面与磁感应强度为B的匀强磁场垂直,导轨电阻不计.金属棒ab棒质量为m,接入电路的电阻为R,并与两导轨始终保持垂直且良好接触,使棒ab由静止开始沿导轨下滑,当流过ab棒某一横截面的电量为q时,它的速度大小为v,则金属棒ab在这一过程中( )| A. | 棒ab运动的平均速度大小为$\frac{1}{2}$v | |
| B. | 滑行距离为$\frac{qR}{BL}$ | |
| C. | 产生的焦耳热为$\frac{mgqR}{BL}$sinθ-$\frac{1}{2}$mv2 | |
| D. | 受到的最大安培力大小为$\frac{{B}^{2}{L}^{2}v}{R}$sinθ |
分析 金属棒ab由静止开始沿导轨下滑,做加速度逐渐减小的变加速运动.由运动学公式,法拉第电磁感应定律、能量守恒定律等研究处理.
解答 解:A、金属棒ab开始做加速度逐渐减小的变加速运动,不是匀变速直线运动,平均速度不等于$\frac{1}{2}$v,故A错误;
B、通过ab棒截面的电量 q=$\overline{I}$t=$\frac{\overline{E}}{R}$t=$\frac{BL\overline{v}t}{R}$=$\frac{BLS}{R}$,则知ab棒滑行距离为 S=$\frac{qR}{BL}$,故B正确.
C、根据能量守恒得:棒产生的焦耳热为 Q=mgSsinθ-$\frac{1}{2}m{v}^{2}$=$\frac{mgqR}{BL}$sinθ-$\frac{1}{2}m{v}^{2}$,故C正确.
D、导体棒速度为v时,产生的感应电流最大,受到的安培力最大,最大安培力为 F=BIL=B$\frac{BLv}{R}$L=$\frac{{B}^{2}{L}^{2}v}{R}$.故D错误.
故选:BC.
点评 本题根据棒的运动情况,结合图象的物理意义分析位移关系时,要抓住速度图象的斜率等于加速度;同时要结合功能关系进行分析;感应电量与棒运动位移有关,常常知道电量可求位移,或知道位移,可求电量,这种思路要熟悉.

练习册系列答案
相关题目
9.下面说法正确的是( )
| A. | 对于万有引力定律的表达式F=$\frac{G{m}_{1}{m}_{2}}{{r}^{2}}$中G为引力常量,它是由牛顿通过实验测得 | |
| B. | 对于万有引力定律的表达式F=$\frac{G{m}_{1}{m}_{2}}{{r}^{2}}$中m1、m2受到的引力是一对平衡力 | |
| C. | 行星绕恒星的运动轨道如果是圆形,那么所有行星运行周期T的平方与轨道半径r的三次方的比为常数,设$\frac{{r}^{3}}{{T}^{2}}$=K,则常数K的大小与恒星的质量及行星的质量有关 | |
| D. | 行星绕恒星的运动轨道如果是圆形,那么所有行星运行周期T的平方与轨道半径r的三次方的比为常数,设$\frac{{r}^{3}}{{T}^{2}}$=K,则常数K的大小只与恒星的质量有关 |
15.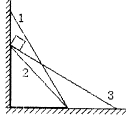 将三个木板1、2、3固定在墙角,木板与墙壁和地面构成了三个不同的三角形,如图所示,其中1与2底边相同,2和3高度相同.现将一个可以视为质点的物块分别从三个木板的顶端由静止释放,并沿木板下滑到底端,物块与木板之间的动摩擦因数μ均相同.在这三个过程中,下列说法正确的是( )
将三个木板1、2、3固定在墙角,木板与墙壁和地面构成了三个不同的三角形,如图所示,其中1与2底边相同,2和3高度相同.现将一个可以视为质点的物块分别从三个木板的顶端由静止释放,并沿木板下滑到底端,物块与木板之间的动摩擦因数μ均相同.在这三个过程中,下列说法正确的是( )
 将三个木板1、2、3固定在墙角,木板与墙壁和地面构成了三个不同的三角形,如图所示,其中1与2底边相同,2和3高度相同.现将一个可以视为质点的物块分别从三个木板的顶端由静止释放,并沿木板下滑到底端,物块与木板之间的动摩擦因数μ均相同.在这三个过程中,下列说法正确的是( )
将三个木板1、2、3固定在墙角,木板与墙壁和地面构成了三个不同的三角形,如图所示,其中1与2底边相同,2和3高度相同.现将一个可以视为质点的物块分别从三个木板的顶端由静止释放,并沿木板下滑到底端,物块与木板之间的动摩擦因数μ均相同.在这三个过程中,下列说法正确的是( )| A. | 沿着1和2下滑到底端时,物块的速度不同;沿着2和3下滑到底端时,物块的速度相同 | |
| B. | 沿着1下滑到底端时,物块的速度最大 | |
| C. | 物块沿着3下滑到底端的过程中,产生的热量是最多的 | |
| D. | 物块沿着1和2下滑到底端的过程中,产生的热量是一样多的 |
12.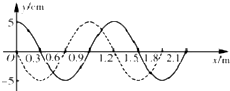 一列沿x轴传播的简谐横波,t=0时刻的波形如图中实线所示,t=0.2s时刻的波形如图中的虚线所示,则( )
一列沿x轴传播的简谐横波,t=0时刻的波形如图中实线所示,t=0.2s时刻的波形如图中的虚线所示,则( )
 一列沿x轴传播的简谐横波,t=0时刻的波形如图中实线所示,t=0.2s时刻的波形如图中的虚线所示,则( )
一列沿x轴传播的简谐横波,t=0时刻的波形如图中实线所示,t=0.2s时刻的波形如图中的虚线所示,则( )| A. | 各质点均沿x轴方向运动 | B. | 波的周期可能是$\frac{4}{15}$s | ||
| C. | 波的频率可能为1.25Hz | D. | 波的传播速度可能为4.5m/s |
19. 如图所示,在竖直放置的半圆形容器的中心O点分别以水平初速度v1、v2抛出两个小球(可视为质点),最终它们分别落在圆弧上的A点和B点,已知OA与OB互相垂直,且OA与竖直方向成α角,则两小球初速度之比为( )
如图所示,在竖直放置的半圆形容器的中心O点分别以水平初速度v1、v2抛出两个小球(可视为质点),最终它们分别落在圆弧上的A点和B点,已知OA与OB互相垂直,且OA与竖直方向成α角,则两小球初速度之比为( )
 如图所示,在竖直放置的半圆形容器的中心O点分别以水平初速度v1、v2抛出两个小球(可视为质点),最终它们分别落在圆弧上的A点和B点,已知OA与OB互相垂直,且OA与竖直方向成α角,则两小球初速度之比为( )
如图所示,在竖直放置的半圆形容器的中心O点分别以水平初速度v1、v2抛出两个小球(可视为质点),最终它们分别落在圆弧上的A点和B点,已知OA与OB互相垂直,且OA与竖直方向成α角,则两小球初速度之比为( )| A. | tanα | B. | sinα | C. | tanα$\sqrt{tanα}$ | D. | cosα |
9.关于一定量的理想气体,下列叙述正确的是:( )
| A. | 气体对外做功,其内能一定减少 | |
| B. | 先等温膨胀,再等容升温可以使压强回到初始值 | |
| C. | 绝热压缩过程,其温度必升高 | |
| D. | 在完全失重的情况下,密闭容器内的气体对器壁没有压强 |
13.为了探测X星球,一探测飞船在该星球上空绕其做匀速圆周运动时,经过时间t,飞船行程为s,飞船与X星球中心连线扫过的角是θ弧度,万有引力常量为G,X星球半径为R,则可推知X星球密度的表达式是( )
| A. | $\frac{3{t}^{2}θ}{4πG{s}^{3}{R}^{3}}$ | B. | $\frac{3{s}^{3}}{4θπG{t}^{2}{R}^{3}}$ | C. | $\frac{4θπ{R}^{3}G{t}^{2}}{3{s}^{3}}$ | D. | $\frac{4π{R}^{3}G{s}^{3}}{3θ{t}^{2}}$ |
14.对于地球同步卫星的认识,正确的是( )
| A. | 同步卫星可在我国北京上空运行,常用于我国的电视转播 | |
| B. | 运行的角速度大于地球自转角速度 | |
| C. | 所有同步卫星的轨道半径都相同,它们均以第一宇宙速度运行 | |
| D. | 只能在赤道的正上方,所有国家的同步卫星的轨道均相同 |
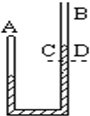 如图所示,竖直放置的U形管在A侧用水银封有一定质量的空气,B端开口向上,其中水银面高于A侧.在温度保持不变的条件下,若将B端管子上部沿图中CD虚线截去.在水银面稳定后,被封闭气体的体积增大.压强将减小.若从B端缓慢注入少量水银,稳定后,U形管左右液面的高度差将增大.(选填“增大”、“不变”或“减小”)
如图所示,竖直放置的U形管在A侧用水银封有一定质量的空气,B端开口向上,其中水银面高于A侧.在温度保持不变的条件下,若将B端管子上部沿图中CD虚线截去.在水银面稳定后,被封闭气体的体积增大.压强将减小.若从B端缓慢注入少量水银,稳定后,U形管左右液面的高度差将增大.(选填“增大”、“不变”或“减小”)