题目内容
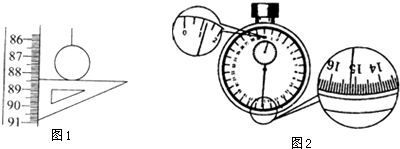
19. 如图所示,在竖直放置的半圆形容器的中心O点分别以水平初速度v1、v2抛出两个小球(可视为质点),最终它们分别落在圆弧上的A点和B点,已知OA与OB互相垂直,且OA与竖直方向成α角,则两小球初速度之比为( )
如图所示,在竖直放置的半圆形容器的中心O点分别以水平初速度v1、v2抛出两个小球(可视为质点),最终它们分别落在圆弧上的A点和B点,已知OA与OB互相垂直,且OA与竖直方向成α角,则两小球初速度之比为( )| A. | tanα | B. | sinα | C. | tanα$\sqrt{tanα}$ | D. | cosα |
分析 由几何关系可知两球下落高度及水平位移的关系,再由平抛运动的规律可求得初速度之比.
解答 解:由几何关系可知,A的竖直位移为:hA=Rcosα,水平位移为:xA=Rsinα;
B的竖直位移为:hB=Rcos(90°-α)=Rsinα,水平位移为:xB=Rsin(90°-α)=Rcosα
由平抛运动的规律可知:h=$\frac{1}{2}g{t}^{2}$,x=v0t
解得:v0=x$\sqrt{\frac{g}{2h}}$
则 $\frac{{v}_{1}}{{v}_{2}}$=$\frac{{x}_{A}}{{x}_{B}}$•$\sqrt{\frac{{h}_{B}}{{h}_{A}}}$=tanα $\sqrt{tanα}$
故选:C.
点评 本题考查平抛运动规律的应用,解题的关键在于明确题意及几何关系,运用运动学公式解答.

练习册系列答案
相关题目
4.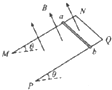 如图,足够长的U型光滑金属导轨平面与水平面成θ角(0<θ<90°),其中MN和PQ平行且间距为L,导轨平面与磁感应强度为B的匀强磁场垂直,导轨电阻不计.金属棒ab棒质量为m,接入电路的电阻为R,并与两导轨始终保持垂直且良好接触,使棒ab由静止开始沿导轨下滑,当流过ab棒某一横截面的电量为q时,它的速度大小为v,则金属棒ab在这一过程中( )
如图,足够长的U型光滑金属导轨平面与水平面成θ角(0<θ<90°),其中MN和PQ平行且间距为L,导轨平面与磁感应强度为B的匀强磁场垂直,导轨电阻不计.金属棒ab棒质量为m,接入电路的电阻为R,并与两导轨始终保持垂直且良好接触,使棒ab由静止开始沿导轨下滑,当流过ab棒某一横截面的电量为q时,它的速度大小为v,则金属棒ab在这一过程中( )
 如图,足够长的U型光滑金属导轨平面与水平面成θ角(0<θ<90°),其中MN和PQ平行且间距为L,导轨平面与磁感应强度为B的匀强磁场垂直,导轨电阻不计.金属棒ab棒质量为m,接入电路的电阻为R,并与两导轨始终保持垂直且良好接触,使棒ab由静止开始沿导轨下滑,当流过ab棒某一横截面的电量为q时,它的速度大小为v,则金属棒ab在这一过程中( )
如图,足够长的U型光滑金属导轨平面与水平面成θ角(0<θ<90°),其中MN和PQ平行且间距为L,导轨平面与磁感应强度为B的匀强磁场垂直,导轨电阻不计.金属棒ab棒质量为m,接入电路的电阻为R,并与两导轨始终保持垂直且良好接触,使棒ab由静止开始沿导轨下滑,当流过ab棒某一横截面的电量为q时,它的速度大小为v,则金属棒ab在这一过程中( )| A. | 棒ab运动的平均速度大小为$\frac{1}{2}$v | |
| B. | 滑行距离为$\frac{qR}{BL}$ | |
| C. | 产生的焦耳热为$\frac{mgqR}{BL}$sinθ-$\frac{1}{2}$mv2 | |
| D. | 受到的最大安培力大小为$\frac{{B}^{2}{L}^{2}v}{R}$sinθ |
11.一定质量的理想气体,经过下列变化后,温度可以回到初始状态温度的是( )
| A. | 先等容降压,再等压压缩 | B. | 先等压压缩,再等容降压 | ||
| C. | 先等容升压,再等压膨胀 | D. | 先等压膨胀,再等容降压 |
9.下列现象中,不是由于液体的表面张力而引起的是( )
| A. | 小昆虫能在水面上自由走动 | |
| B. | 融化的蜡烛从燃烧的蜡烛上流下来,冷却后呈球形 | |
| C. | 小孩吹出肥皂泡 | |
| D. | 树叶能飘浮在水面上 |
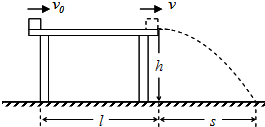 如图所示,质量为m的可视为质点的小物块在粗糙水平桌面上做直线运动,经距离l后以速度v飞离桌面,最终落在水平地面上.已知l=1.4m,v=3.0m/s,m=0.10kg,物块与桌面间的动摩擦因数?=0.25,桌面高h=0.45m.不计空气阻力,重力加速度取10m/s2.求:
如图所示,质量为m的可视为质点的小物块在粗糙水平桌面上做直线运动,经距离l后以速度v飞离桌面,最终落在水平地面上.已知l=1.4m,v=3.0m/s,m=0.10kg,物块与桌面间的动摩擦因数?=0.25,桌面高h=0.45m.不计空气阻力,重力加速度取10m/s2.求:
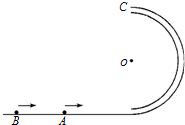 如图所示,半径为R,内径很小的光滑半圆细管竖直放置,两个质量均为m的小球A、B,以不同的速率进入管内,若A球通过圆周最高点C,对管壁上部的压力为3mg,B球通过最高点C时,对管壁内侧下部的压力为0.75mg,求A、B球落地点间的距离.(不计一切阻力)
如图所示,半径为R,内径很小的光滑半圆细管竖直放置,两个质量均为m的小球A、B,以不同的速率进入管内,若A球通过圆周最高点C,对管壁上部的压力为3mg,B球通过最高点C时,对管壁内侧下部的压力为0.75mg,求A、B球落地点间的距离.(不计一切阻力)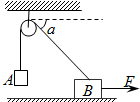 如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦),在用水平变力F拉物体B沿水平方向向右以2m/s的速度作匀速直线运动的过程中,绳子的拉力>物体A的重力(填“>”“=”“<”),当α=60°时,则物体A的速度大小1m/s.
如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦),在用水平变力F拉物体B沿水平方向向右以2m/s的速度作匀速直线运动的过程中,绳子的拉力>物体A的重力(填“>”“=”“<”),当α=60°时,则物体A的速度大小1m/s.