题目内容
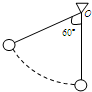
长为1m的轻绳，上端固定在O点，下端连一质量为 0.5kg的小球．若小球在竖直平面内摆动过程中，轻绳偏离竖直线的最大角度为60°，求：（1）小球在最低点时的速度；
（2）小球经过最低点时绳的张力．
分析：（1）小球下落过程机械能守恒，根据机械能守恒定律列式即可求解；
（2）在最低点，由牛顿第二定律列式即可求解．
（2）在最低点，由牛顿第二定律列式即可求解．
解答：解：（1）小球下落过程机械能守恒，选取最低点为零势能参考平面，
则，mgL（1-cosθ）=
mv2
解得：v=
m/s
（2）在最低点，由牛顿第二定律得
F-mg=m
解得 F=10N
答：（1）小球在最低点时的速度为
m/s；
（2）小球经过最低点时绳的张力伟10N
则，mgL（1-cosθ）=
| 1 |
| 2 |
解得：v=
| 10 |
（2）在最低点，由牛顿第二定律得
F-mg=m
| v2 |
| L |
解得 F=10N
答：（1）小球在最低点时的速度为
| 10 |
（2）小球经过最低点时绳的张力伟10N
点评：解决本题的关键知道小球做圆周运动向心力的来源，运用牛顿第二定律和动能定理综合求解．
练习册系列答案
相关题目
如图所示，固定斜面的倾角θ=30°，物体A与斜面之间的动摩擦因数为μ=
，轻弹簧下端固定在斜面底端，弹簧处于原长时上端位于C点．用一根不可伸长的轻绳通过轻质光滑的定滑轮连接物体A和B，滑轮右侧绳子与斜面平行，A的质量为4kg，
B的质量为2kg，初始时物体A到C点的距离为L=1m.现给A、B一初速度v0=3m/s使A开始沿斜面向下运动，B向上运动，物体A将弹簧压缩到最短后又恰好能弹到C点．已知重力加速度为g=10m/s2，不计空气阻力，整个过程中，轻绳始终处于伸直状态，求此过程中：
