题目内容
如图所示,固定斜面的倾角θ=30°,物体A与斜面之间的动摩擦因数为μ=![]() ,轻弹簧下端固定在斜面底端,弹簧处于原长时上端位于C点.用一根不可伸长的轻绳通过轻质光滑的定滑轮连接物体A和B,滑轮右侧绳子与斜面平行,A的质量为4kg,
,轻弹簧下端固定在斜面底端,弹簧处于原长时上端位于C点.用一根不可伸长的轻绳通过轻质光滑的定滑轮连接物体A和B,滑轮右侧绳子与斜面平行,A的质量为4kg,![]() B的质量为2kg,初始时物体A到C点的距离为L=1m.现给A、B一初速度v0=3m/s使A开始沿斜面向下运动,B向上运动,物体A将弹簧压缩到最短后又恰好能弹到C点.已知重力加速度为g=10m/s2,不计空气阻力,整个过程中,轻绳始终处于伸直状态,求此过程中:
B的质量为2kg,初始时物体A到C点的距离为L=1m.现给A、B一初速度v0=3m/s使A开始沿斜面向下运动,B向上运动,物体A将弹簧压缩到最短后又恰好能弹到C点.已知重力加速度为g=10m/s2,不计空气阻力,整个过程中,轻绳始终处于伸直状态,求此过程中:
(1)物体A沿斜面向下运动时的加速度大小;
(2)物体A向下运动刚到C点时的速度大小;
(3)弹簧的最大压缩量和弹簧中的最大弹性势能.

解析 (1)a=2.5m/s2
(2)A和斜面间的滑动摩擦力f=2μmgcos θ,物体A向下运动到C点的过程中,根据能量关系有:v=![]() =2m/s.
=2m/s.
(3)从物体A接触弹簧,将弹簧压缩到最短后又恰回到C点,对系统应用动能定理,
-f·2x=0-![]() ×3mv2,x=
×3mv2,x=![]() -
-![]() =0.4m
=0.4m
(3)弹簧从压缩最短到恰好能弹到C点的过程中,对系统根据能量关系有
Ep+mgx=2mgxsin θ+fx
因为mgx=2mgxsin θ所以Ep=fx=![]() mv
mv![]() -
-![]() μmgL.=6J
μmgL.=6J

练习册系列答案
相关题目
 如图所示,固定斜面的倾角为30°,现用平行于斜面的力F拉着质量为m的物体沿斜面向上运动,物体的加速度大小为a,若该物体放在斜面上沿斜面下滑时的加速度大小也为a,则力F的大小是( )
如图所示,固定斜面的倾角为30°,现用平行于斜面的力F拉着质量为m的物体沿斜面向上运动,物体的加速度大小为a,若该物体放在斜面上沿斜面下滑时的加速度大小也为a,则力F的大小是( ) 如图所示,固定在水平地面的倾角为θ斜面上,有一个竖直的挡板,质量为m的光滑圆柱处于静止状态.求:
如图所示,固定在水平地面的倾角为θ斜面上,有一个竖直的挡板,质量为m的光滑圆柱处于静止状态.求: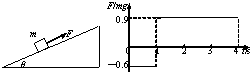 如图所示,固定斜面的倾角为θ=37°,物体与斜面间的动摩擦因数为μ=0.25,物体受到平行于斜面的力F作用静止开始运动,力F随时间t变化规律如图(以平行于斜面向上为正方向),前4s内物体运动的最大加速度大小为
如图所示,固定斜面的倾角为θ=37°,物体与斜面间的动摩擦因数为μ=0.25,物体受到平行于斜面的力F作用静止开始运动,力F随时间t变化规律如图(以平行于斜面向上为正方向),前4s内物体运动的最大加速度大小为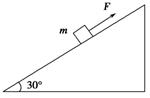
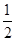 mg B.mg C.
mg B.mg C.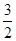 mg D.
mg D.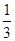 mg
mg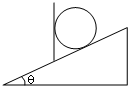 如图所示,固定在水平地面的倾角为θ斜面上,有一个竖直的挡板,质量为m的光滑圆柱处于静止状态.求:
如图所示,固定在水平地面的倾角为θ斜面上,有一个竖直的挡板,质量为m的光滑圆柱处于静止状态.求: