题目内容
16. 如图所示,弹簧的一端固定在竖直墙上,质量为2m的光滑弧形槽静止放在足够长的光滑水平面上,弧形槽末端与水平面相切.一个质量为m的小球从弧形槽上高h处由静止释放,小球与弹簧发生作用的过程中无机械能损失,重力加速度为g.求:
如图所示,弹簧的一端固定在竖直墙上,质量为2m的光滑弧形槽静止放在足够长的光滑水平面上,弧形槽末端与水平面相切.一个质量为m的小球从弧形槽上高h处由静止释放,小球与弹簧发生作用的过程中无机械能损失,重力加速度为g.求:(1)小球与弹簧相互作用过程中,弹簧对小球的冲量大小;
(2)小球与弹簧第一次分离后在弧形槽上能上升的最大高度.
分析 小球与槽组成的系统在水平方向动量守恒,应用动量守恒定律与机械能守恒定律求出球与槽的速度,然后应用动量定理求出小球受到的冲量;应用机械能守恒定律求出小球上升的最大高度.
解答 解:(1)设小球到达水平面时速度大小为v1,槽速度大小为v2,
球与槽组成的系统在水平方向动量守恒,以向右为正方向,
球下滑过程中,由动量守恒定律得:mv1-2mv2=0 ①
由机械能守恒定律的:$mgh=\frac{1}{2}mv_1^2+\frac{1}{2}•2mv_2^2$ ②
解得:${v_1}=2\sqrt{\frac{gh}{3}}$,${v_2}=\sqrt{\frac{gh}{3}}$ ③
在小球与弹簧发生作用的过程中,由动量守恒定律得:
${I_弹}=△{P_球}=-m{v_1}-m{v_1}=2m{v_1}=-4m\sqrt{\frac{gh}{3}}$ ④
即弹簧对小球的冲量大小是:$4m\sqrt{\frac{gh}{3}}$;
(2)小球和槽组成的系统水平方向动量守恒,以向右为正方向,
由动量守恒定律得:mv1+2mv2=(2m+m)v共 ⑤
由机械能守恒定律得:$\frac{1}{2}mv_1^2+\frac{1}{2}×2mv_2^2=\frac{1}{2}(2m+m)v_共^2+mgh'$ ⑥
解得:$h'=\frac{1}{9}h$ ⑦
答:(1)小球与弹簧相互作用过程中,弹簧对小球的冲量大小为$4m\sqrt{\frac{gh}{3}}$;
(2)小球与弹簧第一次分离后在弧形槽上能上升的最大高度是$\frac{1}{9}$h.
点评 本题考查了求冲量、小球上升的高度问题,分析清楚物体的运动过程是正确解题的前提与关键,应用动量守恒定律、机械能守恒定律、动量定理即可正确解题.

 2013年6月11日17时38分,我国利用“神舟十号”飞船将聂海胜、张晓光、王亚平三名宇航员送入太空.设宇航员测出自己绕地球做匀速圆周运动的周期为T,离地高度为H,地球半径为R,则根据T、H、R和引力常量G,能计算出的物理量是( )
2013年6月11日17时38分,我国利用“神舟十号”飞船将聂海胜、张晓光、王亚平三名宇航员送入太空.设宇航员测出自己绕地球做匀速圆周运动的周期为T,离地高度为H,地球半径为R,则根据T、H、R和引力常量G,能计算出的物理量是( )| A. | 地球的质量 | B. | 地球的平均密度 | ||
| C. | 飞船所需的向心力 | D. | 飞船线速度的大小 |
 在同一匀强磁场中,两个完全相同的矩形闭合金属线圈分别以不同的转速,绕与磁感线垂直的轴匀速转动,产生的交变电动势图象如图中曲线a、b所示.则( )
在同一匀强磁场中,两个完全相同的矩形闭合金属线圈分别以不同的转速,绕与磁感线垂直的轴匀速转动,产生的交变电动势图象如图中曲线a、b所示.则( )| A. | t=0时刻穿过两线圈的磁通量均为零 | |
| B. | 曲线a表示的交变电动势有效值为15V | |
| C. | 曲线a表示的交变电动势频率为50Hz | |
| D. | 曲线a、b对应的线圈转速之比为3:2 |
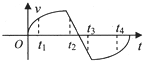
| A. | t1和t2时刻质点运动方向相反 | |
| B. | t1和t4时刻质点加速度方向相反 | |
| C. | t2~t3时间内质点加速度恒定不变 | |
| D. | t1~t2和t3~t4时间质点位移方向相同 |
| A. | 液晶具有流动性、光学性质各向异性 | |
| B. | 在太空大课堂中处于完全失重状态的水滴呈现球形,是由液体表面张力引起的 | |
| C. | 热量总是自发的从分子平均动能大的物体传递到分子平均动能小的物体 | |
| D. | 如果气体分子总数不变,而气体温度升高,则气体分子的平均动能一定增大,气体压强一定增大 | |
| E. | 某气体分子的体积是V0,阿伏伽德罗常数为NA,则标准状态下该气体的摩尔体积为NAV0 |
| A. | 若甲最先抛球,则一定是v甲>v乙 | |
| B. | 若乙最先抛球,则一定是v甲>v乙 | |
| C. | 无论甲乙谁先抛球,只要乙最后接球,就应是v甲>v乙 | |
| D. | 无论怎样抛球和接球,都是v甲>v乙 |
| A. | 若mA>mB,则A对B的万有引力大于B对A的万有引力 | |
| B. | 若mA>mB,则A对B的万有引力小于B对A的万有引力 | |
| C. | 若mA<mB,则A它们之间相互作用的万有引力所产生的加速度aA>aB | |
| D. | 当A、B紧靠在一起时,它们之间的万有引力为无穷大 |
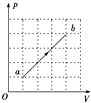
| A. | 气体在a状态的内能比b状态的内能大 | |
| B. | 气体向外释放热量 | |
| C. | 外界对气体做正功 | |
| D. | 气体分子撞击器壁的平均作用力增大 |
