题目内容
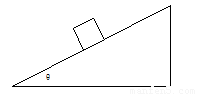
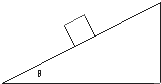 某物体放在一倾角为θ的斜面上,向下轻轻一推,它刚好能匀速下滑.若给此物体一个沿斜面向上的初速度v0,那么
某物体放在一倾角为θ的斜面上,向下轻轻一推,它刚好能匀速下滑.若给此物体一个沿斜面向上的初速度v0,那么(1)物体与斜面间的动摩擦因数μ为多大?
(2)它能沿斜面向上滑的最大位移为多少?
分析:(1)物体沿斜面匀速下滑,受到重力、支持力和滑动摩擦力处于平衡,根据共点力平衡求出支持力和滑动摩擦力,再根据f=μN求出动摩擦因数.
(2)物体沿斜面上滑时受重力、支持力和滑动摩擦力,求出物体的合力,根据牛顿第二定律求出加速度,运用匀变速直线运动的速度位移公式求出上滑的最大距离.
(2)物体沿斜面上滑时受重力、支持力和滑动摩擦力,求出物体的合力,根据牛顿第二定律求出加速度,运用匀变速直线运动的速度位移公式求出上滑的最大距离.
解答:解:(1)刚好能匀速下滑,沿斜面方向上合力为零,根据共点力平衡得:
N=mgcosθ,f=mgsinθ
由f=μN得:μ=
=
=tanθ
(2)物体沿斜面上滑的合力为:F合=mgsinθ+μmgcosθ=2mgsinθ
设它能沿斜面向上滑的最大位移s,根据动能定理得:
F合s=
m
即:2mgsinθ?s=
m
解得::s=
答:(1)物体与斜面间的动摩擦因数为tanθ.
(2)它能沿斜面向上滑的最大位移为
.
N=mgcosθ,f=mgsinθ
由f=μN得:μ=
| f |
| N |
| mgsinθ |
| mgcosθ |
(2)物体沿斜面上滑的合力为:F合=mgsinθ+μmgcosθ=2mgsinθ
设它能沿斜面向上滑的最大位移s,根据动能定理得:
F合s=
| 1 |
| 2 |
| v | 2 0 |
即:2mgsinθ?s=
| 1 |
| 2 |
| v | 2 0 |
解得::s=
| ||
| 4gsinθ |
答:(1)物体与斜面间的动摩擦因数为tanθ.
(2)它能沿斜面向上滑的最大位移为
| ||
| 4gsinθ |
点评:解决本题的关键是知道匀速直线运动的物体所受合力为零,以及知道加速度是联系力学和运动学的桥梁.

练习册系列答案
相关题目