题目内容
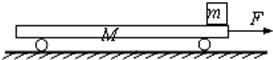 如图质量M=8㎏的小车放在光滑水平面上,在小车右端施加一水平恒力F=8N.当小车向右运动速度达到3m/s时,在小车的右端轻轻放上一质量m=2kg的小物块,物块与小车间的动摩擦因数μ=0.2,小物块始终不离开小车,问:
如图质量M=8㎏的小车放在光滑水平面上,在小车右端施加一水平恒力F=8N.当小车向右运动速度达到3m/s时,在小车的右端轻轻放上一质量m=2kg的小物块,物块与小车间的动摩擦因数μ=0.2,小物块始终不离开小车,问:(1)小车至少要多长?
(2)从小物块放在小车上开始计时,经过3s时间,摩擦力对小物块做的功Wf和拉力F对小车做的功WF分别是多少?(g取10m/s2)
分析:(1)分别对滑块和平板车进行受力分析,根据牛顿第二定律求出各自加速度,物块在小车上停止相对滑动时,速度相同,即可以求出时间,从而求出小车的最小长度;
(2)先求出物块3s末的速度,对木块运用动能定理即可求解摩擦力做功,求出小车3s内的位移,根据恒力做功公式即可求解.
(2)先求出物块3s末的速度,对木块运用动能定理即可求解摩擦力做功,求出小车3s内的位移,根据恒力做功公式即可求解.
解答:解:(1)根据牛顿第二定律得,物块的加速度a1=
=μg=2m/s2,
小车的加速度a2=
=
m/s2=0.5m/s2.
设经过t时间小物块与小车的速度相同,有:a1t=v0+a2t
解得t=
=
s=2s.
此时物块的位移x1=
a1t2=
×2×4m=4m
小车的位移x2=v0t+
a2t2=3×2+
×0.5×4m=7m.
小车至少的长度L=x2-x1=7-4m=3m.
(2)2s末两物体的速度相同,大小v=a1t=4m/s,然后物块和小车一起做匀加速直线运动.
根据牛顿第二定律得,a=
=
m/s2=0.8m/s2.
3末物块的速度v′=v+at′=4+0.8×1m/s=4.8m/s.
根据动能定理得,Wf=
mv2-0=
×2×4.82J=23.04J.
小车在前2s内的位移为7m,后1s内的位移x3=vt′+
at′2=4×1+
×0.8×1m=4.4m.
则小车在前3s内的位移x=7+4.4m=11.4m.
所以恒力F所做的功WF=Fx=8×11.4J=91.2J.
答:(1)小车至少长度为3m;
(2)摩擦力对小物块做的功为23.04J.拉力F对小车所做的功为91.2J.
| μmg |
| m |
小车的加速度a2=
| F-μmg |
| M |
| 8-0.2×20 |
| 8 |
设经过t时间小物块与小车的速度相同,有:a1t=v0+a2t
解得t=
| v0 |
| a1-a2 |
| 3 |
| 2-0.5 |
此时物块的位移x1=
| 1 |
| 2 |
| 1 |
| 2 |
小车的位移x2=v0t+
| 1 |
| 2 |
| 1 |
| 2 |
小车至少的长度L=x2-x1=7-4m=3m.
(2)2s末两物体的速度相同,大小v=a1t=4m/s,然后物块和小车一起做匀加速直线运动.
根据牛顿第二定律得,a=
| F |
| M+m |
| 8 |
| 10 |
3末物块的速度v′=v+at′=4+0.8×1m/s=4.8m/s.
根据动能定理得,Wf=
| 1 |
| 2 |
| 1 |
| 2 |
小车在前2s内的位移为7m,后1s内的位移x3=vt′+
| 1 |
| 2 |
| 1 |
| 2 |
则小车在前3s内的位移x=7+4.4m=11.4m.
所以恒力F所做的功WF=Fx=8×11.4J=91.2J.
答:(1)小车至少长度为3m;
(2)摩擦力对小物块做的功为23.04J.拉力F对小车所做的功为91.2J.
点评:该题是相对运动的典型例题,要认真分析两个物体的受力情况,正确判断两物体的运动情况,再根据运动学基本公式求解,难度适中.

练习册系列答案
相关题目
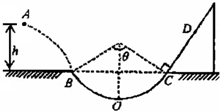 如图所示,将一质量m=1kg的小物块以一定的初速度从A点水平抛出,恰好无碰撞地沿圆弧切线从B点进入光滑的竖直平面内圆弧轨道运动.圆弧的两端点B、C连线水平.小物块离开C点后恰能无碰撞地沿固定斜面向上运动,经0.8s通过D点.己知圆弧半径R=1.0m,圆弧对应的圆心角θ=106°,轨道最低点为O,A点距水平面的高度h=0.8m,小物块与斜面间的动摩擦因数μ=
如图所示,将一质量m=1kg的小物块以一定的初速度从A点水平抛出,恰好无碰撞地沿圆弧切线从B点进入光滑的竖直平面内圆弧轨道运动.圆弧的两端点B、C连线水平.小物块离开C点后恰能无碰撞地沿固定斜面向上运动,经0.8s通过D点.己知圆弧半径R=1.0m,圆弧对应的圆心角θ=106°,轨道最低点为O,A点距水平面的高度h=0.8m,小物块与斜面间的动摩擦因数μ=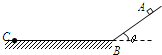 如图所示,质量m=1kg的小物体从倾角θ=37°的光滑斜面上A点静止开始下滑,经B点后进入粗糙水平面(经过B点时速度大小不变而方向变为水平).AB=3m.求:
如图所示,质量m=1kg的小物体从倾角θ=37°的光滑斜面上A点静止开始下滑,经B点后进入粗糙水平面(经过B点时速度大小不变而方向变为水平).AB=3m.求: 如图所示,质量m=1kg的小物体从倾角θ=37°的光滑斜面上A点静止开始下滑,经过B点后进入粗糙水平面,物体经过B点时速度大小不变而方向变为水平,AB=3m,g=10m/s2.试求:
如图所示,质量m=1kg的小物体从倾角θ=37°的光滑斜面上A点静止开始下滑,经过B点后进入粗糙水平面,物体经过B点时速度大小不变而方向变为水平,AB=3m,g=10m/s2.试求: