题目内容
8.如图所示,光滑水平面上有一长度适当的小车,该小车质量为M=5kg,小车右端有一半径R=0.5m光滑圆弧轨道,圆弧轨道最低点和小车上表面在同一高度.质量m=1kg的物块(视为质点)以v0=10m/s的速度从左侧滑上小车,带动小车运动,物块运动到轨道最低点后冲上光滑圆轨道,小车继续沿水平面向右滑行,物块沿圆弧轨道运动恰好到达圆轨道最高点,已知物块与小车之间动摩擦因数μ=0.4,取g=10m/s2,求: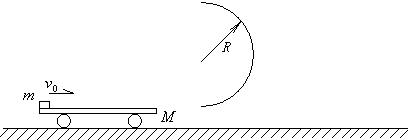
(1)物块冲上圆轨道最低点速度大小v1;
(2)物块冲上圆轨道最低点时小车的速度v2大小;
(3)物块相对小车滑行距离s.
分析 (1)小物块在最高点时,重力恰好提高向心力;此后对圆周运动过程根据动能定理列式求解最低点速度;
(2)滑块滑上小车后,小车和滑块系统水平方向不受外力,故系统动量守恒;
(3)对小车和滑块整体根据公式f•S相对=Q列式求解即可.
解答 解:(1)小物块在最高点时重力提供向心力,得
mg=m$\frac{{v}^{2}}{R}$
解得:
v=$\sqrt{gR}$=$\sqrt{10×0.5}=\sqrt{5}m/s$
在圆周运动过程,根据动能定理,有:
-mg(2r)=$\frac{1}{2}m{v}^{2}-\frac{1}{2}m{v}_{1}^{2}$
解得:
${v}_{1}=\sqrt{{v}^{2}+4gr}=\sqrt{5+4×10×0.5}=5m/s$
(2)物块滑上小车的后,由于水平面光滑,故物块与小车组成系统动量守恒,故:
mv0=mv1+Mv2
代入数据,解得:
v1=1m/s
(3)对物块和小车组成系统,根据动能定理得:
$μmg•S=\frac{1}{2}m{v}_{0}^{2}-(\frac{1}{2}m{v}_{1}^{2}+\frac{1}{2}M{v}_{2}^{2})$
解得:
S=8.75m
答:(1)物块冲上圆轨道最低点速度大小v1为5m/s;
(2)物块冲上圆轨道最低点时小车的速度v2大小为1m/s;
(3)物块相对小车滑行距离S为8.75m.
点评 本题关键是圆周运动和连接体问题的综合问题,关键是明确运动情况和受力情况,根据功能关系、向心力公式和动量守恒定律综合列式求解,不难.

练习册系列答案
相关题目
18.两个偏振片紧靠在一起,将它们放在一盏白炽灯的前面以致没有光通过.如果将其中的一个偏振片旋转180°,在旋转过程中,将会产生下述的哪一种现象( )
| A. | 透过偏振片的光强先增强,然后又减弱到零 | |
| B. | 透过偏振片的光强先增强,然后减弱到非零的最小值 | |
| C. | 透过偏振片的光强在整个过程中都增强 | |
| D. | 透过偏振片的光强先增强,再减弱,然后又增强 |
16.下列说法正确的是( )
| A. | 用光照射某种金属,有光电子从金属表面逸出,如果光的频率不变,而减弱光的强度,则逸出的光电子数减少,光电子的最大初动能不变 | |
| B. | X射线的衍射实验,证实了物质波假设是正确的 | |
| C. | 发生光电效应时,光电子的最大初动能与入射光的频率成正比 | |
| D. | 在康普顿效应中,当入射光子与晶体中的电子碰撞时,把一部分动量转移给电子,因此光子散射后波长变长 | |
| E. | 速度相等的电子和质子,电子的波长大 |
13. 在伦敦奥运会中,牙买加选手博尔特是公认的世界飞人,在男子100m决赛和男子200m决赛中分别以9.63s和19.32s的成绩获得两枚金牌.关于他在这两次决赛中的运动情况,下列说法正确的是( )
在伦敦奥运会中,牙买加选手博尔特是公认的世界飞人,在男子100m决赛和男子200m决赛中分别以9.63s和19.32s的成绩获得两枚金牌.关于他在这两次决赛中的运动情况,下列说法正确的是( )
 在伦敦奥运会中,牙买加选手博尔特是公认的世界飞人,在男子100m决赛和男子200m决赛中分别以9.63s和19.32s的成绩获得两枚金牌.关于他在这两次决赛中的运动情况,下列说法正确的是( )
在伦敦奥运会中,牙买加选手博尔特是公认的世界飞人,在男子100m决赛和男子200m决赛中分别以9.63s和19.32s的成绩获得两枚金牌.关于他在这两次决赛中的运动情况,下列说法正确的是( )| A. | 200m决赛中的路程是100m决赛的两倍 | |
| B. | 200m决赛中的平均速度约为10.35m/s | |
| C. | 100m决赛中的平均速度约为10.38m/s | |
| D. | 100m决赛中的最大速度约为20.76m/s |
20.某电场的电场线分布如图所示,以下说法正确的是( )
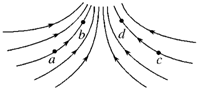

| A. | c点场强大于b点场强 | |
| B. | a点电势低于b点电势 | |
| C. | 若将一试探电荷+q由a点释放,它将沿电场线运动到b点 | |
| D. | 将一试探电荷+q由a移至b的过程中,电势能减小 |
17.做直线运动的甲、乙两物体的位移--时间图象如图所示,则( )
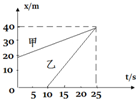

| A. | 当乙开始运动时,两物体相距20m | |
| B. | 在0~10s这段时间内,物体间的距离逐渐变小 | |
| C. | 在10s~25s这段时间内,物体间的距离逐渐变小 | |
| D. | 两物体在10s时相距最远,在25s时相遇 |
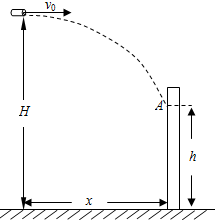 消防车的供水系统主要由水泵、输水管道和水枪组成.如图所示,消防水枪离地高度为H,建筑物上的火点A距地面高为h=60m,水枪与火点的水平距离为x,水泵的功率为P,整个供水系统的效率η=0.6.假设水从水枪水平射出,不计空气阻力,取g=10m/s2.
消防车的供水系统主要由水泵、输水管道和水枪组成.如图所示,消防水枪离地高度为H,建筑物上的火点A距地面高为h=60m,水枪与火点的水平距离为x,水泵的功率为P,整个供水系统的效率η=0.6.假设水从水枪水平射出,不计空气阻力,取g=10m/s2. 质量m=0.5kg的木块静止于水平面上,现在恒力F作用下做匀加速直线运动,已知恒力大小F=5N,方向与水平方向成θ=37°角斜向上,如图所示.2s末撤去此拉力时,木块已滑行的距离s0=12m,(重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.)求:
质量m=0.5kg的木块静止于水平面上,现在恒力F作用下做匀加速直线运动,已知恒力大小F=5N,方向与水平方向成θ=37°角斜向上,如图所示.2s末撤去此拉力时,木块已滑行的距离s0=12m,(重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.)求: