题目内容
【题目】如图所示，边长为L的正六边形abcdef中，存在垂直该平面向内的匀强磁场，磁感应强度大小为B．a点处的粒子源发出大量质量为m、电荷量为+q的同种粒子，粒子的速度大小不同，方向始终垂直ab边且与磁场垂直，不计粒子的重力，当粒子的速度为v时，粒子恰好经过b点，下列说法正确的是 ( )
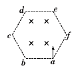
A. 速度小于v的粒子在磁场中运动时间为
B. 经过d点的粒子在磁场中运动的时间为
C. 经过c点的粒子在磁场中做圆周运动的半径为2L
D. 速度大于2v 小于4v的粒子一定打在cd边上
【答案】D
【解析】
A、粒子在磁场中做匀速圆周运动，当粒子的速度为v时，粒子恰好经过b点时在磁场中运动了半周，运动时间为
，轨迹半径等于ab的一半.当粒子的速度小于v时，由
知，粒子的轨迹半径小于ab的一半，仍运动半周，运动时间仍为；故A错误.
B、在a点粒子的速度与ad连线的夹角为30°，粒子经过d点时，粒子的速度与ad连线的夹角也为30°，则粒子轨迹对应的圆心角等于60°，在磁场中运动的时间
；故B错误.
C、经过c点的粒子，根据几何知识知，该粒子在磁场中做圆周运动的圆心b，半径为L，故C错误.
D、设经过b、c、d三点的粒子速度分别为v1、v2、v3．轨迹半径分别为r1、r2、r3．据几何知识可得，
，r2=L，r3=2L，由半径公式得：v2=2v1=2v，v3=4v1=4v，所以只有速度在这个范围：2v≤v≤4v的粒子才打在cd边上；故D正确.
故选D.
练习册系列答案
相关题目
