题目内容
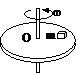
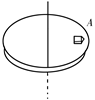
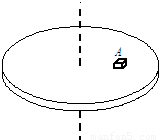
如图所示，在绕竖直轴匀速转动的水平圆盘盘面上，离轴心r=20 cm处放置一小物块A，其质量为m＝2 kg，A与盘面间相互作用的静摩擦力的最大值为其重力的k倍（k＝0.5），试求：
（1）当圆盘转动的角速度ω＝2 rad/s时，物块与圆盘间的摩擦力大小为多大？方向如何？
（2）欲使A与盘面间不发生相对滑动，则圆盘转动的最大角速度为多大？（取g=10 m/s2）
（1）当圆盘转动的角速度ω＝2 rad/s时，物块与圆盘间的摩擦力大小为多大？方向如何？
（2）欲使A与盘面间不发生相对滑动，则圆盘转动的最大角速度为多大？（取g=10 m/s2）
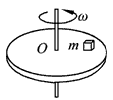
解：（1）物体随圆盘一起绕轴线转动，需要向心力，而竖直方向物体受到的重力mg、支持力FN不可能提供向心力，向心力只能来源于圆盘对物体的静摩擦力
根据牛顿第二定律可求出物体受到的静摩擦力的大小：Ff=F向=mω2r=2×22×0.2 N=1.6 N，方向沿半径指向圆心
（2）欲使物块与盘不发生相对滑动，做圆周运动的向心力应不大于最大静摩擦力。即F向=mrωm2≤kmg
解得ωm≤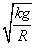
=
rad/s=5 rad/s.
根据牛顿第二定律可求出物体受到的静摩擦力的大小：Ff=F向=mω2r=2×22×0.2 N=1.6 N，方向沿半径指向圆心
（2）欲使物块与盘不发生相对滑动，做圆周运动的向心力应不大于最大静摩擦力。即F向=mrωm2≤kmg
解得ωm≤
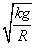=rad/s=5 rad/s.
练习册系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
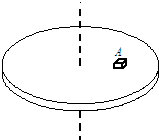（2005?南京一模）如图所示，在绕竖直轴匀速转动的水平圆盘盘面上，离轴心r=20cm处放置一小物块A，其质量为m=2kg，A与盘面间相互作用的静摩擦力的最大值为其重力的k倍（k=0.5），试求：
