题目内容
6.小船在200m宽的河中横渡,水流速度为2m/s,船在静水中的航速是4m/s,求:(1)当小船的船头始终正对对岸时,它将在何时、何处到达对岸?
(2)要使小船到达正对岸,应如何行驶(即船头与河岸的夹角为多大)?历时多长?
分析 (1)当船头始终正对对岸时,根据t=$\frac{d}{{v}_{c}}$求出渡河的时间,再由位移公式,求得到达对岸的位置;
(2)要使小船到达正对岸,即合速度的方向与河岸垂直,根据平行四边形定则,求出合速度的大小,并由几何关系,结合矢量合成法则,即可求解.
解答 解:小船参与了两个运动:随水漂流和船在静水中的运动.由分运动的等时性和独立性,
(1)小船渡河时间等于垂直于河岸的分运动时间:
t=t1=$\frac{d}{v船}$=$\frac{200}{4}$ s=50 s,
沿河流方向的位移x水=v水t=2×50 m=100 m,
即在正对岸下游100 m处靠岸. 
(2)要小船垂直过河,即合速度应垂直于河岸,如图所示,
则cosθ=$\frac{v水}{v船}$=$\frac{2}{4}$=$\frac{1}{2}$,
所以θ=60°,即航向与岸上游成60°角;
渡河时间t=$\frac{d}{v合}$=$\frac{d}{v船sinθ}$=$\frac{200}{4sin60°}$ s=$\frac{100}{\sqrt{3}}$ s≈57.7 s.
答:(1)50 s后在正对岸下游100 m处靠岸;
(2)航向与岸上游成60°角,时间为57.7 s.
点评 解决本题的关键知道运动的合成和分解遵循平行四边形定则,以及知道当合速度的方向与河岸垂直,小船将垂直到达对岸.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.短跑运动员在100m的比赛中,测得他在5s末的速度是8.7m/s,10s末到达终点时的速度为10.3m/s,此运动员在这100m中有关说法正确的是( )
| A. | 运动员在这100m中的平均速度是(8.7m/s+10.3m/s)/2=9.5m/s | |
| B. | 运动员在这100m中的平均速度是10m/s | |
| C. | 10.3m/s为瞬时速度 | |
| D. | 不能求出前5秒平均速度 |
1.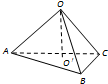 如图所示,真空空间中四点O、A、B、C恰为棱长为a的正四面体的四个顶点,其中A、B、C三点在水平面上,O′为三角形ABC的几何中心.已知静电力常量为k,重力加速度为g,下列说法中正确的是( )
如图所示,真空空间中四点O、A、B、C恰为棱长为a的正四面体的四个顶点,其中A、B、C三点在水平面上,O′为三角形ABC的几何中心.已知静电力常量为k,重力加速度为g,下列说法中正确的是( )
 如图所示,真空空间中四点O、A、B、C恰为棱长为a的正四面体的四个顶点,其中A、B、C三点在水平面上,O′为三角形ABC的几何中心.已知静电力常量为k,重力加速度为g,下列说法中正确的是( )
如图所示,真空空间中四点O、A、B、C恰为棱长为a的正四面体的四个顶点,其中A、B、C三点在水平面上,O′为三角形ABC的几何中心.已知静电力常量为k,重力加速度为g,下列说法中正确的是( )| A. | 若A、B、C三点各固定电荷量为+Q的点电荷,则O点电势比O′点高 | |
| B. | 若A、B、C三点各固定电荷量为+Q的点电荷,将质量为m的带正电小球(可视为点电荷)放置在O点恰静止,则小球所带电荷量为$\frac{\sqrt{6}mg{a}^{2}}{6kQ}$ | |
| C. | 若A、B、C三点各固定电荷量为-Q的点电荷,则O点与AB、BC、AC三边中点的电势差相等 | |
| D. | 若A、B、C三点各固定电荷量为-Q的点电荷,则O点场强比O′点大 |
11.关于合力和分力的说法正确的是( )
| A. | 合力一定大于每一个分力 | B. | 合力一定介于两个分力之间 | ||
| C. | 合力可以等于其中一个分力 | D. | 合力就是两个分力之和 |
18.利用电流表和电压表测定一节干电池的电动势和内电阻.要求尽量减小实验误差.
(1)应该选择的实验电路是图1中的甲(选项“甲”或“乙”).

(2)现有电流表、开关和导线若干,以及以下器材:
A.电压表(0~15V) B.电压表(0~3V)
C.滑动变阻器(0~50Ω) D.滑动变阻器(0~500Ω),
实验中电压表应选用B;滑动变阻器应选用c;(选填相应器材前的字母)
(3)某位同学记录的6组数据如表所示,其中5组数据的对应点已经标在图2的坐标纸上,请标出余下一组数据的对应点,并画出U-I图线.
(4)根据(3)中所画图线可得出干电池的电动势E=1.5v,内电阻r=0.83Ω
(5)实验中,随着滑动变阻器滑片的移动,电压表的示数U以及干电池的输出功率P都会发生变化.图3的各示意图中正确反映P-U关系的是C.

(1)应该选择的实验电路是图1中的甲(选项“甲”或“乙”).

(2)现有电流表、开关和导线若干,以及以下器材:
A.电压表(0~15V) B.电压表(0~3V)
C.滑动变阻器(0~50Ω) D.滑动变阻器(0~500Ω),
实验中电压表应选用B;滑动变阻器应选用c;(选填相应器材前的字母)
(3)某位同学记录的6组数据如表所示,其中5组数据的对应点已经标在图2的坐标纸上,请标出余下一组数据的对应点,并画出U-I图线.
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 电压U(V) | 1.45 | 1.40 | 1.30 | 1.25 | 1.20 | 1.10 |
| 电流 ( A ) | 0.060 | 0.120 | 0.240 | 0.260 | 0.360 | 0.480 |
(5)实验中,随着滑动变阻器滑片的移动,电压表的示数U以及干电池的输出功率P都会发生变化.图3的各示意图中正确反映P-U关系的是C.

15. 长度为0.2m的轻杆OA,A端有一质量为1.0kg的小球,小球以O点为圆心,在竖直平面内做圆周运动,通过最高点时小球的速率为1.0m/s,则此时轻杆OA受到(g=10m/s2)( )
长度为0.2m的轻杆OA,A端有一质量为1.0kg的小球,小球以O点为圆心,在竖直平面内做圆周运动,通过最高点时小球的速率为1.0m/s,则此时轻杆OA受到(g=10m/s2)( )
 长度为0.2m的轻杆OA,A端有一质量为1.0kg的小球,小球以O点为圆心,在竖直平面内做圆周运动,通过最高点时小球的速率为1.0m/s,则此时轻杆OA受到(g=10m/s2)( )
长度为0.2m的轻杆OA,A端有一质量为1.0kg的小球,小球以O点为圆心,在竖直平面内做圆周运动,通过最高点时小球的速率为1.0m/s,则此时轻杆OA受到(g=10m/s2)( )| A. | 5N的压力 | B. | 5N的拉力 | C. | 15N的压力 | D. | 15N的拉力 |
14.通电螺线管内有一在磁场力作用下处于静止的小磁针,磁针指向如图所示,则( )
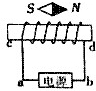

| A. | 螺线管的c端为N极,a接电源的正极 | B. | 螺线管的c端为N极,a接电源的负极 | ||
| C. | 螺线管的d端为S极,a接电源的正极 | D. | 螺线管的d端为S极,a接电源的负极 |
 在“用油膜法估测分子大小”实验中所用的油酸酒精溶液的浓度为1 000mL溶液中有纯油酸0.6mL,用注射器测得1mL上述溶液为80滴,把1滴该溶液滴入盛水的浅盘内,让油膜在水面上尽可能散开,测得油酸薄膜的轮廓形状和尺寸如图所示,图中正方形方格的边长为1cm.
在“用油膜法估测分子大小”实验中所用的油酸酒精溶液的浓度为1 000mL溶液中有纯油酸0.6mL,用注射器测得1mL上述溶液为80滴,把1滴该溶液滴入盛水的浅盘内,让油膜在水面上尽可能散开,测得油酸薄膜的轮廓形状和尺寸如图所示,图中正方形方格的边长为1cm.