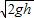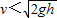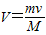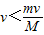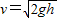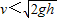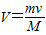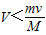Question

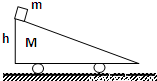
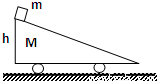
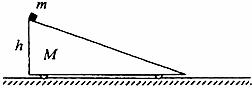
斜面小车的质量为M，高为h，一个质量为m的物体从小车的顶点滑下，物块滑离斜面小车底端时的速度设为v，不计一切摩擦，下列说法：
①物块滑离小车时的速度v=

2gh

②物块滑离小车时的速度v＜

2gh

③物块滑离小车时小车的速度V=

mv

M

④物块滑离小车时小车的速度V＜

mv

M

其中正确的是（　　）

A．只有①③正确

B．只有①④正确

C．只有②③正确

D．只有②④正确

Answer 1

分析：物体在下降的过程中，物体和小车再水平方向上的动量守恒，根据根据动量来分析即可．

解答：解：根据物体和小车在水平方向上的动量守恒，取向右为正，可得
0=mv_水平-MV，
所以V=

mv水平

M

，
由于v_水平＜v，所以物块滑离小车时小车的速度V＜

mv

M

，所以④正确；
当小车不动的时候，根据机械能守恒可得，
mgh=

1

2

mv²，
所以v=

2gh

，
由于小车的运动，根据能量的守恒可知，物块滑离小车时的速度v＜

2gh

，所以②正确．
故选D．

点评：本题属于在某方向上动量的守恒，物块在下降的过程中，水平方向上的动量是守恒的，但是整体的动量不守恒．