题目内容
由于激光是亮度高、平行度好、单色性好的相干光,所以光导纤维中用激光作高速传输信息的载体.要使射到粗细均匀的圆形光导纤维的一个端面上的激光束都能从另一个端面射出,而不会从侧壁“泄漏”出来,那么光导纤维所用的材料的折射率至少应是多少呢?
假设激光束在光导纤维前端的入射角为θ1,折射角为θ2,折射光线射向侧面时的入射角为θ3,如图36所示.
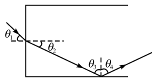
图36
由折射定律有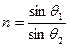 ,由几何关系θ2+θ3=90°,则sinθ2=cosθ3.又由全反射临界角公式得sinθ3=
,由几何关系θ2+θ3=90°,则sinθ2=cosθ3.又由全反射临界角公式得sinθ3=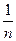 ,故cosθ3=
,故cosθ3=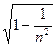 .要保证从端面射入的光线都能发生全反射,应有θ1=90°时,射到光导纤维侧壁上的光线也会发生全反射.
.要保证从端面射入的光线都能发生全反射,应有θ1=90°时,射到光导纤维侧壁上的光线也会发生全反射.
故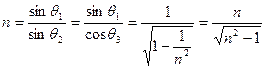
得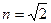 .
.
本题也可利用分析的方法:由图可看出:θ1越大,θ2越大,而θ2+θ3=90°,则θ3越小,射到光纤侧壁上的光越不容易全反射,当θ1等于90°时,此时θ3为临界角,此时θ2=θ3=45°
折射率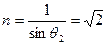 .
.

图36
由折射定律有
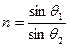 ,由几何关系θ2+θ3=90°,则sinθ2=cosθ3.又由全反射临界角公式得sinθ3=
,由几何关系θ2+θ3=90°,则sinθ2=cosθ3.又由全反射临界角公式得sinθ3=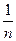 ,故cosθ3=
,故cosθ3=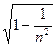 .要保证从端面射入的光线都能发生全反射,应有θ1=90°时,射到光导纤维侧壁上的光线也会发生全反射.
.要保证从端面射入的光线都能发生全反射,应有θ1=90°时,射到光导纤维侧壁上的光线也会发生全反射.故
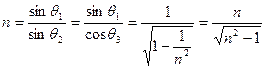
得
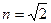 .
.本题也可利用分析的方法:由图可看出:θ1越大,θ2越大,而θ2+θ3=90°,则θ3越小,射到光纤侧壁上的光越不容易全反射,当θ1等于90°时,此时θ3为临界角,此时θ2=θ3=45°
折射率
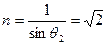 .
.
练习册系列答案
相关题目




 激发态的氢原子向低能级跃迁,发出的光照射到一块等腰三角形玻璃棱镜AB面上,从AC面出射的光线将照射到一块金属板上,如图1所示.若只考虑第一次照射到AC面的光线,则下列说法中正确的是( )
激发态的氢原子向低能级跃迁,发出的光照射到一块等腰三角形玻璃棱镜AB面上,从AC面出射的光线将照射到一块金属板上,如图1所示.若只考虑第一次照射到AC面的光线,则下列说法中正确的是( )
 能级跃迁到基态发出的光
能级跃迁到基态发出的光