题目内容
简谐横波某时刻的波形如图甲所示,从该时刻开始计时,波上A质点的振动图象如图乙所示.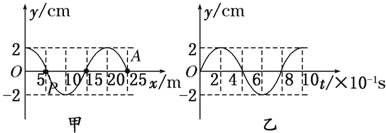
(1)求该简谐波的波速;
(2)从该时刻起,再经过△t=0.4s,P质点通过的路程和波传播的距离分别为多少?
(3)若t=0时振动刚刚传到A点,从该时刻起再经多长时间图甲中横坐标为45m的质点(未画出)第二次位于波峰?

(1)求该简谐波的波速;
(2)从该时刻起,再经过△t=0.4s,P质点通过的路程和波传播的距离分别为多少?
(3)若t=0时振动刚刚传到A点,从该时刻起再经多长时间图甲中横坐标为45m的质点(未画出)第二次位于波峰?
分析:先据图象知,λ=20m,T=0.8s,用波速公式求出波速;用s=v△t求波传播的距离,利用△t=0.4s=
,求出质点P通过的路程;横坐标为45m的质点(未画出)第二次位于波峰,即质点在坐标原点的波形传播到为45m的质点处,利用t=
求解即可.
| T |
| 2 |
| s |
| t |
解答:解:(1)据图象知,λ=20m,T=0.8s,A=2cm.
所以波速v=
=
m/s=25 m/s.
(2)因为△t=0.4 s=
,
所以质点P通过的路程为2A=4 cm.
在
内波传播的距离为
=10 m.
(3)由A点t=0时刻向上振动知,波沿x轴正方向传播,波速v=25 m/s.
x=45 m处的质点第一次到达波峰的时间
t1=
s=1 s
此质点第二次位于波峰的时间t=t1+T=1.8 s.
答:(1)求该简谐波的波速25m/s;
(2)从该时刻起,再经过△t=0.4s,P质点通过的路程为4cm和波传播的距离10m;
(3)若t=0时振动刚刚传到A点,从该时刻起再经1.8s时间图甲中横坐标为45m的质点(未画出)第二次位于波峰.
所以波速v=
| λ |
| T |
| 20 |
| 0.8 |
(2)因为△t=0.4 s=
| T |
| 2 |
所以质点P通过的路程为2A=4 cm.
在
| T |
| 2 |
| λ |
| 2 |
(3)由A点t=0时刻向上振动知,波沿x轴正方向传播,波速v=25 m/s.
x=45 m处的质点第一次到达波峰的时间
t1=
| 45-20 |
| 25 |
此质点第二次位于波峰的时间t=t1+T=1.8 s.
答:(1)求该简谐波的波速25m/s;
(2)从该时刻起,再经过△t=0.4s,P质点通过的路程为4cm和波传播的距离10m;
(3)若t=0时振动刚刚传到A点,从该时刻起再经1.8s时间图甲中横坐标为45m的质点(未画出)第二次位于波峰.
点评:灵活应用波动图象和质点的振动图象求波速是解题的关键,注意质点的振动路程和波传播的距离的区别;明确波传播的实质.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 (2008?嘉定区二模)一列沿x轴传播的简谐横波某时刻的波形图象如图甲所示.若从此时刻开始计时,则图乙表示a、b、c、d中哪个质点的振动图象( )
(2008?嘉定区二模)一列沿x轴传播的简谐横波某时刻的波形图象如图甲所示.若从此时刻开始计时,则图乙表示a、b、c、d中哪个质点的振动图象( ) 简谐横波某时刻的波形如图示,P为介质中的一个质点,以下说法正确的是( )
简谐横波某时刻的波形如图示,P为介质中的一个质点,以下说法正确的是( )
