题目内容
9.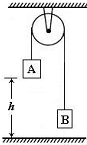 如图所示,两个质量各为m1和m2的小物块A和B,分别系在一条跨过定滑轮的轻细软绳两端,己知ml>m2.现要利用此装置验证机械能守恒定律.选定物块A从静止开始下落的过程进行测量.若已测定的物理量有:物块的质量m1、m2;物块A下落的距离h及下落这段距离所用的时间t.
如图所示,两个质量各为m1和m2的小物块A和B,分别系在一条跨过定滑轮的轻细软绳两端,己知ml>m2.现要利用此装置验证机械能守恒定律.选定物块A从静止开始下落的过程进行测量.若已测定的物理量有:物块的质量m1、m2;物块A下落的距离h及下落这段距离所用的时间t.①物体A下落h距离时的速度v=$\frac{2h}{t}$.
②本实验需要验证系统重力势能的减少量△EP=(m1-m2)gh与系统动能的增加量△AEK=_$\frac{2({m}_{1}+{m}_{2}){h}^{2}}{{t}^{2}}$是否相等.
分析 ①应用匀变速直线运动的推论求出A下落高度h时的速度;
②根据重力势能的计算公式求出系统减少的重力势能,由动能的计算公式求出系统增加的重力势能.
解答 解:①A向下做初速度为零的匀加速直线运动,下落距离h过程的平均速度:$\overline{v}$=$\frac{h}{t}$,
由匀变速直线运动的推论可知,该过程中间时刻的瞬时速度:v中间=$\overline{v}$=$\frac{h}{t}$,
速度:v中间=$\frac{{v}_{0}+v}{2}$=$\frac{0+v}{2}$=$\frac{v}{2}$,则A下落高度h时的速度:v=2v中间=$\frac{2h}{t}$;
②系统重力势能的减少量△EP=(m1-m2)gh;
系统动能的增加量△AEK=$\frac{1}{2}$(m1+m2)v2=$\frac{2({m}_{1}+{m}_{2}){h}^{2}}{{t}^{2}}$;
故答案为:①$\frac{2h}{t}$;②(m1-m2)gh;$\frac{{2({m_1}+{m_2}){h^2}}}{t^2}$.
点评 本题考查了求物体的速度、系统减少的重力势能、增加的动能,分析清楚物体运动过程、求出物体A的速度是解题的关键,应用重力势能与动能的计算公式可以解题;本题的难点是求出A下落h时的瞬时速度.

练习册系列答案
相关题目
19. 如图所示,张华同学骑自行车下坡虽然不在蹬车,人和自行车却运动得越来越快.张华下坡过程中( )
如图所示,张华同学骑自行车下坡虽然不在蹬车,人和自行车却运动得越来越快.张华下坡过程中( )
 如图所示,张华同学骑自行车下坡虽然不在蹬车,人和自行车却运动得越来越快.张华下坡过程中( )
如图所示,张华同学骑自行车下坡虽然不在蹬车,人和自行车却运动得越来越快.张华下坡过程中( )| A. | 重力势能减少,动能减少 | B. | 重力势能减少,动能增加 | ||
| C. | 重力势能增加,动能减少 | D. | 重力势能增加,动能增加 |
20. 如图,曲线a和直线b分别是在同一平直公路上行驶的汽车a和b的速度-时间(v-t)图线.已知在t1时刻两车第一次相遇,由图可知( )
如图,曲线a和直线b分别是在同一平直公路上行驶的汽车a和b的速度-时间(v-t)图线.已知在t1时刻两车第一次相遇,由图可知( )
 如图,曲线a和直线b分别是在同一平直公路上行驶的汽车a和b的速度-时间(v-t)图线.已知在t1时刻两车第一次相遇,由图可知( )
如图,曲线a和直线b分别是在同一平直公路上行驶的汽车a和b的速度-时间(v-t)图线.已知在t1时刻两车第一次相遇,由图可知( )| A. | 在时刻t1,b车追上a车 | |
| B. | 在时刻t2,两车第二次相遇 | |
| C. | 在时刻t2,a、b两车加速度方向相反 | |
| D. | 在t1到t2时间内,两车的平均速度相等 |
14.将质量为2m的长木板静止地放在光滑水平面上,如图甲所示.第一次,可视为质点的质量为m的小铅块,在木板上以水平初速度v0由木板左端开始向右运动,恰能滑至木板的右端与木板相对静止;第二次,将木板分成长度与质量均相等的两段1和2,两者紧挨着仍放在此光滑水平面上,让小铅块以相同的初速度v0由木板1的左端开始向右运动,如图乙所示.设小铅块与长木板间的动摩擦因数为μ.重力加速度为g.对上述两过程,下列判断正确的是( )


| A. | 图乙所示过程中,铅块在木板1上滑动时两段木板间的作用力大小为$\frac{1}{2}$μmg | |
| B. | 图乙所示过程中,铅块在木板1上滑动时两段木板间的作用力大小为μmg | |
| C. | 图乙所示过程中,小铅块能到达木板2的右端 | |
| D. | 图甲所示过程中系统因摩擦而产生的热量比图乙所示过程中系统因摩擦而产生的热量多 |
1. 如图所示,质量为m的光滑球放在竖直挡板AB和倾角为α的固定斜面间.当挡板AB绕B端缓慢移动至斜面垂直,则在此过程中( )
如图所示,质量为m的光滑球放在竖直挡板AB和倾角为α的固定斜面间.当挡板AB绕B端缓慢移动至斜面垂直,则在此过程中( )
 如图所示,质量为m的光滑球放在竖直挡板AB和倾角为α的固定斜面间.当挡板AB绕B端缓慢移动至斜面垂直,则在此过程中( )
如图所示,质量为m的光滑球放在竖直挡板AB和倾角为α的固定斜面间.当挡板AB绕B端缓慢移动至斜面垂直,则在此过程中( )| A. | 球对挡板的压力逐渐减小 | B. | 挡板对球的支持力逐渐增大 | ||
| C. | 球对斜面的压力逐渐减小 | D. | 斜面对球的支持力逐渐增大 |
13.下列说法正确的是( )
| A. | 速度变化越大,则加速度越大 | |
| B. | 加速度a<0,则物体的速度一定增大 | |
| C. | 加速度a增大,则物体的速度一定增大 | |
| D. | 若加速度方向与速度方向相同,加速度减小时,则速度反而增大 |
 如图,有一电荷量为-2.0×10-5 C的点电荷从电场中的A点移动到B点,电场力做功为4.8×10-2 J,求AB两点的电势差?电场强度的方向?
如图,有一电荷量为-2.0×10-5 C的点电荷从电场中的A点移动到B点,电场力做功为4.8×10-2 J,求AB两点的电势差?电场强度的方向? 为测量一电源的电动势及内阻,备有以下器材:
为测量一电源的电动势及内阻,备有以下器材: (量程为3V,内阻为3kΩ)
(量程为3V,内阻为3kΩ) 如图所示,R1=R2=R3=8Ω,电容器电容C=5μF,电源电动势E=6V,内阻不计,求开关S由稳定的闭合状态断开后流过R3的电荷量.
如图所示,R1=R2=R3=8Ω,电容器电容C=5μF,电源电动势E=6V,内阻不计,求开关S由稳定的闭合状态断开后流过R3的电荷量.