Question

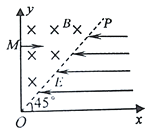
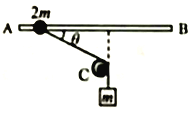
【题目】如图，不可伸长的轻绳跨过光滑定滑轮，一端连接质量为2m的小球(视为质点)，另一端连接质量为m的物块，小球套在光滑的水平杆上。开始时轻绳与杆的夹角为θ，现将小球从图示位置静止释放，当θ=90°时，小球的速度大小为v，此时物块尚未落地。重力加速度大小为g，则

A. 当θ=90°时，物块的速度大小为2v

B. 当θ=90°时，小球所受重力做功的功率为2mgv

C. 在θ从图示位置增大到90°过程中，小球一直向右做加速运动

D. 在θ从图示位置增大到90°过程中，物块一直向下做加速运动

Answer 1

【答案】C

【解析】

根据速度的分解可以计算θ=90°时，物块的速度；根据重力与速度的方向的关系，可以计算重力的做功功率；根据受力与速度的方向的关系，可以判断小球速度的变化；根据θ=90°时，物块的速度为0，可以判断物块速度的变化。

A.设物块和小球的速度大小分别是v1和v2，则有v1=v2cosθ。当θ=90°小球的速度大小为v时，物块的速度为0，故A错误；

B.根据功率P=Fvcosθ，当θ=90°时，小球所受重力做功的功率为0，故B错误；

C. 在θ从图示位置增大到90°过程中，小球一直受到绳子向右下方的拉力，向右做加速运动，故C正确；

D. 当θ=90°时，物块的速度为0，所以在θ从图示位置增大到90°过程中，物块速度先增大后减小，故D错误。

故选：C