题目内容
 两列简谐横波均沿x轴传播,传播速度v大小相等,其中一列沿正x方向传播(如图中实线所示),一列沿负x方向传播(如图中虚线所示).这两列波的频率相等,振动方向均沿y轴,则图中x=1,2,3,4,5,6,7,8各点中振幅最大的是x=
两列简谐横波均沿x轴传播,传播速度v大小相等,其中一列沿正x方向传播(如图中实线所示),一列沿负x方向传播(如图中虚线所示).这两列波的频率相等,振动方向均沿y轴,则图中x=1,2,3,4,5,6,7,8各点中振幅最大的是x=4和8
4和8
,振幅最小的是x=2和6
2和6
.分析:两列波的频率相等,相遇时会产生干涉,当质点到两波源的路程差是半个波长的奇数倍时,振动减弱,振幅等于两列单独引起的振幅之差;当质点到两波源的路程差是半个波长的偶数倍时,振动加强,振幅等于两列单独引起的振幅之和.根据路程差判断质点振动情况,再确定振幅.
解答:解:由题意可知,这两列波的频率相同,在同种均匀介质中相遇会发生干涉现象.设波长为λ,由图看出,处于1、2、3、4、5、6、7、8位置的各质点到两波源P、Q的距离差分别为:
质点1或7的△x1=
λ-
λ=
λ;
质点2或6的△x2=
λ-
λ=
λ;
质点3或5的△x3=
λ-
λ=
λ;
质点4的△x4=λ-λ=0;
质点8的△x8=
λ-
λ=λ.
据干涉时振动加强区域应满足的条件为△x=nλ(n=0,1,2…),可知处于4和8位置的质点振动加强振幅最大;
振动减弱区域应满足的条件为△x=(2n+1)
(n=0,1,2…),可知处于2和6位置的质点的振幅最小.
故答案为:4和8,2和6.
质点1或7的△x1=
| 11 |
| 8 |
| 5 |
| 8 |
| 3 |
| 4 |
质点2或6的△x2=
| 10 |
| 8 |
| 6 |
| 8 |
| 1 |
| 2 |
质点3或5的△x3=
| 9 |
| 8 |
| 7 |
| 8 |
| 1 |
| 4 |
质点4的△x4=λ-λ=0;
质点8的△x8=
| 3 |
| 2 |
| 1 |
| 2 |
据干涉时振动加强区域应满足的条件为△x=nλ(n=0,1,2…),可知处于4和8位置的质点振动加强振幅最大;
振动减弱区域应满足的条件为△x=(2n+1)
| λ |
| 2 |
故答案为:4和8,2和6.
点评:本题根据路程差与波长的关系判断波叠加的结果,也可以根据下列理论进行判断:波峰与波峰相遇或波谷与波谷相遇时振动加强,振幅等于两列波振幅之和;两列波峰与波谷相遇时振幅减弱,振幅等于两列波振幅之差.

练习册系列答案
相关题目
波速均为v=12m/s的两列简谐横波均沿x轴正方向传播,在某时刻它们的波形图分别如图甲和图乙所示,其中P、Q均处于波峰位置.则关于这两列波,下列说法中正确的是( )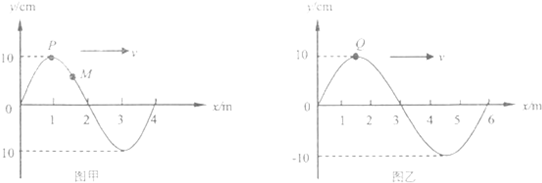

| A、如果这两列波相遇可能产生稳定的干涉现象 | B、从图示时刻开始,图甲中P质点第一次到达平衡位置所经历的时间比图乙中Q质点第一次到达平衡位置所经历的时间短 | C、从图示时刻开始,图甲中P质点比M质点先到达平衡位置 | D、从图示的时刻开始,经过t=0.5s,P、Q质点通过的路程均为40cm |

 (2011?卢湾区模拟)A、B两列简谐横波均沿x轴正向传播,在某时刻的波形分别如图甲、乙所示,经过时间t(t小于A波的周期TA),这两列简谐横波的波形分别变为图丙、丁所示,则A、B两列波的波速vA、vB之比可能为( )
(2011?卢湾区模拟)A、B两列简谐横波均沿x轴正向传播,在某时刻的波形分别如图甲、乙所示,经过时间t(t小于A波的周期TA),这两列简谐横波的波形分别变为图丙、丁所示,则A、B两列波的波速vA、vB之比可能为( )