��Ŀ����
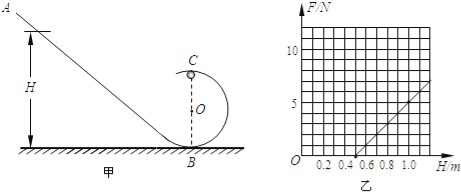
����Ŀ���ڰ뾶R=5000km��ij������棬�Ա��������ʵ�飬ʵ��װ����ͼ����ʾ����ֱƽ���ڵĹ⻬����ɹ��AB��Բ�����BC��ɣ�������m=0.2kg��С�ӹ��AB�ϸ�H����ij�㾲ֹ���£��������������С��C��ʱ�Թ����ѹ��F���ı�H�Ĵ�С���ɲ����Ӧ��F��С��F��H�ı仯��ϵ��ͼ����ʾ����
��1��Բ����İ뾶�����������������ٶȣ�
��2��������ĵ�һ�����ٶȣ�
���𰸡���1��Բ����İ뾶Ϊ0.2m�����������������ٶ�Ϊ5m/s2��
��2������ĵ�һ�����ٶ�Ϊ5��103m/s
�������������������1��С���A��C�˶��Ĺ����У�ֻ��������������е���غ㣬���ݻ�е���غ㶨�ɺ�ţ�ٵڶ��������С��Թ��C���ѹ����H�Ĺ�ϵʽ��Ȼ����F��Hͼ�����Բ����İ뾶�����������������ٶȣ�
��2����һ�����ٶ��������������������Բ���˶����ٶ���ȣ���������������������mg=m![]() ���������ĵ�һ�����ٶȣ�
���������ĵ�һ�����ٶȣ�
�⣺��1��С���C��ʱ����F+mg=m![]()
�ָ���mg��H��2r��=mvC2
�������F=![]() H��5mg
H��5mg
����ͼ��֪��H1="0.5" mʱF1=0��H2="1.0" mʱF2="5" N��
�ɽ��g="5" m/s2
r="0.2" m
��2����m![]() =mg
=mg
�ɵ�v==5��103m/s��
������ĵ�һ�����ٶ�Ϊ5��103m/s��
�𣺣�1��Բ����İ뾶Ϊ0.2m�����������������ٶ�Ϊ5m/s2��
��2������ĵ�һ�����ٶ�Ϊ5��103m/s��

 53���ò�ϵ�д�
53���ò�ϵ�д�