题目内容
(万有引力定律+单摆+圆周运动)有人设想在地球赤道上垂直于地球表面竖起一根刚性的长杆,杆子的长度是地球半径的若干倍.长杆随地球一起自转.在长杆上距地面高度为h=R(R为地球半径)处,悬挂一个摆长为L,质量为m的单摆(L远远小于R).设地球半径R、地球表面的重力加速度g地球的自转周期T0均为已知,
(1)悬挂单摆处随地球自转的向心加速度多大?
(2)该单摆的振动周期为多少?
(3)单摆悬挂于长杆上距地球表面的高度H为多高处,单摆就无法振动?
答案:

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
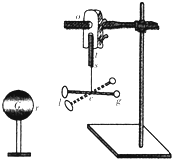 为了验证电荷之间的引力与电荷间距离的平方成反比的规律,库仑还设计了一个电摆实验,其装置如图所示:G为绝缘金属球,lg为虫胶做的小针,悬挂在7~8尺长的蚕丝sc下端,l端放一镀金小圆纸片.G、l间的距离可调.实验时使G、l带异号电荷,则小针受到电引力作用可以在水平面内做小幅摆动.测量出G、l在不同距离时,lg摆动同样次数的时间,从而计算出每次振动的周期.库仑受万有引力定律的启发,把电荷之间的吸引力和地球对物体的吸引力加以类比,猜测电摆振动的周期与带电小纸片l到绝缘带电金属球G之间的距离成正比.库仑记录了三次实验数据如下表: 为了验证电荷之间的引力与电荷间距离的平方成反比的规律,库仑还设计了一个电摆实验,其装置如图所示:G为绝缘金属球,lg为虫胶做的小针,悬挂在7~8尺长的蚕丝sc下端,l端放一镀金小圆纸片.G、l间的距离可调.实验时使G、l带异号电荷,则小针受到电引力作用可以在水平面内做小幅摆动.测量出G、l在不同距离时,lg摆动同样次数的时间,从而计算出每次振动的周期.库仑受万有引力定律的启发,把电荷之间的吸引力和地球对物体的吸引力加以类比,猜测电摆振动的周期与带电小纸片l到绝缘带电金属球G之间的距离成正比.库仑记录了三次实验数据如下表:
(1)根据牛顿万有引力定律和单摆的周期公式可以推断:地面上单摆振动的周期T正比于摆球离开地球表面的距离h. (2)从表格中第1、第2组数据看,电摆的周期与纸片到球心之间的距离可能存在正比例关系. (3)假如电摆的周期与带电纸片到金属球球心距离成正比,则三次测量的周期之比应为20:40:53,但是实验测得值为20:41:60,因此假设不成立. (4)第3组实验测得的周期比预期值偏大,可能是振动时间较长,两带电体漏电造成实验有较大的误差造成的. 则下列选项正确的是( ) |
| A、(2)(4) |
| B、(1)(2)(3)(4) |
| C、(2)(3) |
| D、(1)(3) |

