Question

【题目】传送带以v=6m/s的速度顺时针转动，一小物块轻轻放在传送带左端B点，然后在传送带的带动下，从传送带右端的C点水平抛出，最后落到地面上的D点，己知传送带长度 L=12m，物块与传送带之间的动摩擦因数μ=0.2（g=10m/s2）．

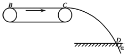
（1）求物块在传送带上运动的时间；

（2）若物块落在D点的速度方向与地面夹角为α=45°，求C点到地面的高度和C、D两点间的水平距离．

Answer 1

【答案】（1）3.5s；（2）1.8m， 3.6m．

【解析】

（1）设物块在传送带上的加速度为a，经过t1时间与传送带速度相同，有：μmg=ma
且 v=at1
解得：t1=3s
设物块在t1时间内的位移为x，由x=at2
代入数据解得：x=9m
因为x＜L2，所以物块还将在传送带上做一段匀速运动，设匀速运动的时间为t2，有：
L2-x=vt2
得：t2=0.5s
则物块在传送带上运动的时间为：t=t1+t2=3s+0.5s=3.5s
（2）物块落在D点的速度方向与地面夹角为：α=45°
则有：tanα=
代入数据解得：vDy=6m/s．
由vDy2=2gh代入数据解得：h=1.8m
设平抛的时间为t3，有vDy=gt3
得：t3=0.6s．
则平抛的水平位移为：x=vCt3
得：x=3.6m