题目内容
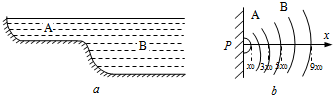
浅水处水波的速度跟水深度有关,其关系式为v=
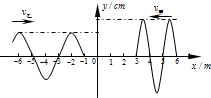
,式中h为深度,g为重力加速度,如图a所示是一个池塘的剖面图,AB两部分深度不同,图b是从上往下俯视,看到从P处向外传播水波波形(弧形实线代表波峰).若已知A处水深20cm,则B处的水深为______cm,B处的水波波长是A处水波波长的______倍.
| gh |

由图看出,A处水波波长为:λA=3x0-x0=2x0.B处水波波长为:λB=9x0-5x0=4x0.
故:λB=2λA
由于水波在水中的频率不变,则由波速公式v=λf得水波在A、B两处波速与波长成正比,则:
=
=
又由题意,水波的速度跟水深度关系为:v=
,则有:
=
=4
解得:hB=4hA=80cm.
故答案为:80,2
故:λB=2λA
由于水波在水中的频率不变,则由波速公式v=λf得水波在A、B两处波速与波长成正比,则:
| vA |
| vB |
| λA |
| λB |
| 1 |
| 2 |
又由题意,水波的速度跟水深度关系为:v=
| gh |
| hB |
| hA |
| ||
|
解得:hB=4hA=80cm.
故答案为:80,2

练习册系列答案
相关题目