题目内容
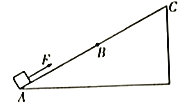
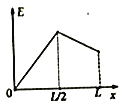
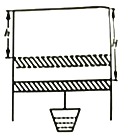
【题目】如图所示，两根平行光滑金属导轨间距为L，导轨电阻不计，下端PQ接有阻值为R的电阻，导轨平面与水平面的夹角为
，且处在磁感应强度大小为B、方向垂直于导轨平面斜向上的匀强磁场中。一质量为m、电阻也为R的导体棒与固定弹簧相连后放在导轨上，静止时导体棒处于导轨的MN处。已知弹簧的劲度系数为k，弹簧的中心轴线与导轨平行。现将导体棒从弹簧处于自然长度时由静止释放，整个运动过程中导体棒始终与导轨垂直并保持良好接触。则下列说法中正确的是
A. 当导体棒沿导轨向下运动时流过电阻R的电流方向为由P到Q
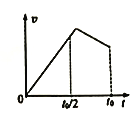
B. 当导体棒的速度最大时，弹簧的伸长量为
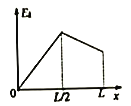
C. 导体棒最终静止时弹簧的弹性势能为EP，则导体棒从开始运动到停止运动的过程中，回路中产生的焦耳热为
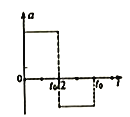
D. 若导体棒第一次运动到MN处时速度为v，则此时导体棒的加速度大小为
【答案】ACD
【解析】
由右手定则可以判断出电流方向；当导体棒所受合力为零时速度最大，应用平衡条件可以求出此时弹簧的伸长量；根据能量守恒定律求出回路产生的焦耳热；根据安培力公式求出导体棒受到的安培力，然后应用牛顿第二定律求出导体棒的加速度.
A．由右手定则可知，当导体棒沿导轨向下运动时流过电阻R的电流方向为由P到Q，故A正确；
B．导体棒所受合力为零，即：重力、弹簧弹力与安培力合力为零时速度最大，弹簧伸长量为
时，弹簧弹力为：mgsinθ，此时导体棒所受合力为安培力，导体棒速度不是最大，故B错误；
C．导体棒最终静止，由平衡条件得：mgsinθ=kx，弹簧伸长量：
，由能量守恒定律得：mgxsinθ=Q+EP，解得：
，故C正确；
D．导体棒到达MN处时，弹簧的弹力：kx=mgsinθ，此时导体棒受到的安培力：
，对导体棒，由牛顿第二定律得：
，解得：
，故D正确；
故选ACD.
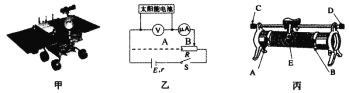
高效智能课时作业系列答案
【题目】某兴趣小组欲通过测定工业污水(含多种重金属离子)的电阻率来判断某工厂废水是否达到排放标准(达标的污水离子浓度低，电阻率大，一般电阻率ρ≥200Ω·m的工业废水即达到排放标准)。图甲所示为该组同学所用圆柱形盛水容器，其左、右两侧面为金属薄板(电阻极小)，其余侧面由绝缘材料制成，左、右两侧带有接线柱。
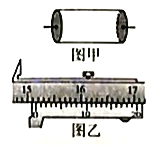
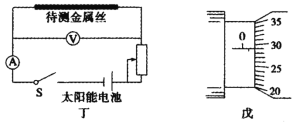
(1)先用刻度尺和游标卡尺分别测量盛水容器的长度L和内径D，某次测量示数如图乙所示，他们的读数分别为：L=40.0cm；D=___________cm。
将水样注满容器后，进行以下操作：
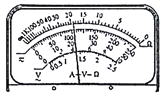
(2)分别用多用电表欧姆挡的“×1k”、“×100”两挡粗测水样的电阻值时，表盘上指针如图丙所示，则所测水样的电阻约为___________Ω。
(3)为更精确地测量所取水样的电阻，该小组从实验室中找到如下实验器材：
A.电流表(量程5mA，电阻RA=800Ω)
B.电压表(量程15V，电阻RV约为10kΩ)
C.滑动变阻器(0~20Ω，额定电流1A)
D.电源(12V，内阻约10Ω)
E.开关一只，导线若干
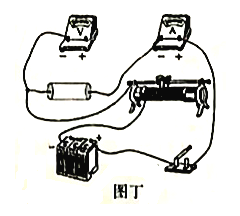
请在图丁中完成电路连接。________________________
(4)正确连接电路后，闭合开关，测得一组U、I数据；再调节滑动变阻器，重复上述测量步骤，得出一系列数据如下表所示。
U/V | 2.0 | 4.0 | 6.0 | 8.0 | 10.0 |
I/mA | 0.73 | 1.43 | 2.17 | 2.89 | 3.58 |
由以上测量数据得到U/I的平均值为2772Ω，则待测水样的电阻为___________Ω。据此可知，所测水样___________排放标准(填“达到”或“没达到”)。
