题目内容
 (2008?上海)在“用单摆测重力加速度”的实验中,
(2008?上海)在“用单摆测重力加速度”的实验中,(1)某同学的操作步骤为:
a.取一根细线,下端系住直径为d的金属小球,上端固定在铁架台上
b.用米尺量得细线长度l
c.在摆线偏离竖直方向5°位置释放小球
d.用秒表记录小球完成n次全振动的总时间t,得到周期T=t/n
e.用公式g=
| 4π2l |
| T2 |
按上述方法得出的重力加速度值与实际值相比
偏小
偏小
(选填“偏大”、“相同”或“偏小”).(2)已知单摆在任意摆角θ时的周期公式可近似为T′=T0[1+asin2(
| θ |
| 2 |
T′、θ
T′、θ
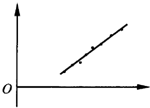
;若某同学在实验中得到了如图所示的图线,则图象中的横轴表示T′
T′
.分析:(1)根据g=
.判断重力加速度的误差.
(2)通过测量不同摆角时摆角θ和对应的周期值T′,由T′=T0[1+asin2(
)]得:sin2(
)=
-
,看sin2(
)-T′是否是线性关系.
| 4π2l |
| T2 |
(2)通过测量不同摆角时摆角θ和对应的周期值T′,由T′=T0[1+asin2(
| θ |
| 2 |
| θ |
| 2 |
| T′ |
| aT0 |
| 1 |
| a |
| θ |
| 2 |
解答:解:(1)在测量摆长时只测出摆线的长度,摆长的测量值偏小,根据g=
,g的测量值偏小.
(2)为了用图象法验证T′=T0[1+asin2(
)],则要测出不同的摆角θ,以及所对应的周期T′.实验中得到的线性图线,根据T′=T0[1+asin2(
)],得sin2(
)=
-
,sin2(
)-T′是一次函数关系.所以图象中的横轴表示T′.
故本题答案为:(1)偏小(2)T′、θ,T′.
| 4π2l |
| T2 |
(2)为了用图象法验证T′=T0[1+asin2(
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| T′ |
| aT0 |
| 1 |
| a |
| θ |
| 2 |
故本题答案为:(1)偏小(2)T′、θ,T′.
点评:解决本题的关键掌握单摆的周期公式T=2π
,会通过g=
,分析因摆长、周期的误差而引起重力加速度的误差.
|
| 4π2l |
| T2 |

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
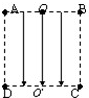 (2008?上海模拟)边长为l的正方形ABCD区域内存在一个有界匀强电场,电场线平行于纸面,场强为E.质量m、带电量+q的某种粒子从AB边中点O以任意平行纸面方向、大小不变的初速度射入电场,仅在电场力作用下运动.若某个粒子从CD边中点离开,则该粒子射入时初速度方向为
(2008?上海模拟)边长为l的正方形ABCD区域内存在一个有界匀强电场,电场线平行于纸面,场强为E.质量m、带电量+q的某种粒子从AB边中点O以任意平行纸面方向、大小不变的初速度射入电场,仅在电场力作用下运动.若某个粒子从CD边中点离开,则该粒子射入时初速度方向为 (2008?上海模拟)如图所示,为一个开口、容积500mL的瓶子,装有400mL水,温度为27℃,大气压为105pa,此时盖上瓶盖后将其降温.
(2008?上海模拟)如图所示,为一个开口、容积500mL的瓶子,装有400mL水,温度为27℃,大气压为105pa,此时盖上瓶盖后将其降温.