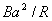题目内容
如图所示,物体A,B通过细绳及轻质弹簧连接在轻滑轮两侧,物体B的质量为2m,放置在倾角为30°的光滑斜面上,物体A的质量为m,用手托着物体A使弹簧处于原长,细绳伸直,A与地面的距离为h,物体B静止在斜面上挡板P处。放手后物体A下落,与地面即将接触时速度大小为v,此时物体B对挡板恰好无压力,则下列说法正确的是( )
A.弹簧的劲度系数为 |
B.此时弹簧的弹性势能等于mgh -  mv2 mv2 |
| C.此时物体A的加速度大小为g,方向竖直向上 |
| D.此后物体B可能离开挡板沿斜面向上运动 |
AB
解析试题分析:由于物块A与地面即将接触时速度大小为v,弹簧的伸长为h,此时物块A是加速向下还是减速向下不容易判断,所以我们就对物块B进行受力分析,由于B此时对档板的压强为零,即B受到的力有重力、弹簧的拉力、斜面对它的支持力,将重力正交分解,可得弹簧对它的拉力F=2mgsin30°=mg,即弹簧受到的拉力也是mg,故弹簧的劲度系数为 ,A是正确的;我们再对刚放手时与A到底端时的两个状态进行对比,运用机械能守恒定律得:mgh=
,A是正确的;我们再对刚放手时与A到底端时的两个状态进行对比,运用机械能守恒定律得:mgh= mv2+Ep,故此时弹簧的弹性势能等于mgh -
mv2+Ep,故此时弹簧的弹性势能等于mgh - mv2,B是正确的;
mv2,B是正确的;
此进A受到弹簧向上的拉力为mg,故A受到的合力为零,其加速度的大小也为零,C不对;当A触底后,弹簧对B的拉力仍为mg,但B只有受到大于mg的拉力时才会离开档板沿斜面向上运动,故此后物体B不可能离开挡板沿斜面向上运动,D也是不对的。
考点:机械能守恒定律,牛顿第二定律,胡克定律等。

如图所示,倾角为θ的足够长传送带以恒定的速率v0沿逆时针方向运行。t=0时,将质量
m=1kg的小物块(可视为质点)轻放在传送带上,物块速度随时间变化的图象如图所示。设沿传送带向下为正方向,取重力加速度g=10m/s2。则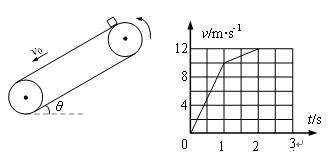
| A.摩擦力的方向始终沿传送带向下 |
| B.1~2s内,物块的加速度为2m/s2 |
| C.传送带的倾角θ=30° |
| D.物体与传送带之间的动摩擦因数μ=0.5 |
如图甲所示,某人正通过定滑轮将质量为m的货物提升到高处.滑轮的质量和摩擦均不计,货物获得的加速度a与绳子对货物竖直向上的拉力T之间的函数关系如图乙所示.由图可以判断 
| A.图线与纵轴的交点M的值aM=-g |
| B.图线与横轴的交点N的值TN=mg |
| C.图线的斜率等于物体的质量m |
D.图线的斜率等于物体质量的倒数 |