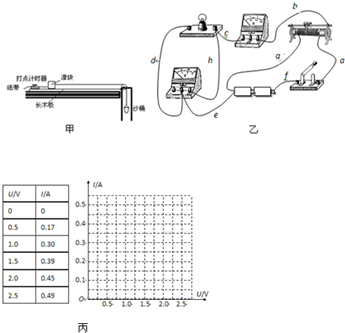
题目内容
一个质量m=0.1kg的正方形金属框总电阻R=0.5Ω，金属框放在表面绝缘且光滑的斜面顶端（金属框上边与AA′重合），自静止开始沿斜面下滑，下滑过程中穿过一段边界与斜面底边BB′平行、宽度为d的匀强磁场后滑至斜面底端（金属框下边与BB′重合），设金属框在下滑过程中的速度为v，与此对应的位移为s，那么v2-s图象如图所示，已知匀强磁场方向垂直斜面向上，g=10m/s2．
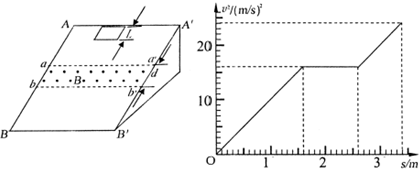
（1）根据v2-s图象所提供的信息，计算出斜面倾角θ和匀强磁场宽度d．
（2）金属框从进入磁场到穿出磁场所用的时间是多少？
（3）匀强磁场的磁感应强度多大？
（1）根据v2-s图象所提供的信息，计算出斜面倾角θ和匀强磁场宽度d．
（2）金属框从进入磁场到穿出磁场所用的时间是多少？
（3）匀强磁场的磁感应强度多大？
（1）由图象可知，从s=0到s1=1.6 m过程中，金属框作匀加速运动
由公式v2=2as可得金属框的加速度 a1=
=
=5m/s2
根据牛顿第二定律 mgsinθ=ma1 θ=30°
金属框下边进磁场到上边出磁场，线框做匀速运动．
∴△s=2L=2d=2.6-1.6=1m，d=L=0.5m
（2）金属框刚进入磁场时，
=16v1=4m/s
金属框穿过磁场所用的时间 t=
=0.25s
（3）因匀速通过磁场 B
L=mgsinθ
所以磁感应强度的大小 B=0.5T
答：（1）斜面的倾角为30°，匀强磁场的宽度为0.5m．
（2）金属框从进入磁场到穿出磁场所用的时间是0.25s．
（3）匀强磁场的磁感应强度为0.5T．
由公式v2=2as可得金属框的加速度 a1=
| ||
| 2s1 |
| 16 |
| 2×1.6 |
根据牛顿第二定律 mgsinθ=ma1 θ=30°
金属框下边进磁场到上边出磁场，线框做匀速运动．
∴△s=2L=2d=2.6-1.6=1m，d=L=0.5m
（2）金属框刚进入磁场时，
| v | 21 |
金属框穿过磁场所用的时间 t=
| 2L |
| v1 |
（3）因匀速通过磁场 B
| BLv1 |
| R |
所以磁感应强度的大小 B=0.5T
答：（1）斜面的倾角为30°，匀强磁场的宽度为0.5m．
（2）金属框从进入磁场到穿出磁场所用的时间是0.25s．
（3）匀强磁场的磁感应强度为0.5T．
练习册系列答案
优加精卷系列答案
相关题目
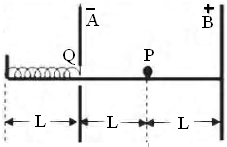如图所示，A、B是两块竖直放置的平行金属板，相距为2L，分别带有等量的正、负电荷，在两板间形电场强度大小为E匀强电场．A板上有一小孔（它的存在对两板间匀强电场分布的影响可忽略不计），孔中有一条与板垂直的水平光滑绝缘轨道，一个质量为m，电荷量为q（q＞0）的小球（可视为质点），在外力作用下静止在轨道的中点P处．一自然长度为L的轻弹簧左端固定在距A板左侧L处挡板上，右端固定一块轻小的绝缘材料制成的薄板Q．撤去外力释放带电小球，它将在电场力作用下由静止开始向左运动，穿过小孔后（不与金属板A接触）与薄板Q一起压缩弹簧，由于薄板Q及弹簧的质量都可以忽略不计，可认为小球与Q接触过程中不损失机械能．小球从接触Q开始，经过一段时间第一次把弹簧压缩至最短，然后又被弹簧弹回．由于薄板Q的绝缘性能有所欠缺，使得小球每次离开Q瞬间，小球的电荷量都损失一部分，而变成刚与Q接触时小球电荷量的
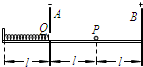如图所示，A、B是两块竖直放置的平行金属板，相距为2l，分别带有等量的负、正电荷，在两板间形成电场强度大小为E的匀强电场．A板上有一小孔（它的存在对两板间匀强电场分布的影响可忽略不计），孔的下沿右侧有一条与板垂直的水平光滑绝缘轨道，一个质量为m、电荷量为q（q＞0）的小球（可视为质点），在外力作用下静止在轨道的中点P处．孔的下沿左侧也有一与板垂直的水平光滑绝缘轨道，轨道上距A板l处有一固定档板，长为l的轻弹簧左端固定在挡板上，右端固定一块轻小的绝缘材料制成的薄板Q．撤去外力释放带电小球，它将在电场力作用下由静止开始向左运动，穿过小孔（不与金属板A接触）后与薄板Q一起压缩弹簧，由于薄板Q及弹簧的质量都可以忽略不计，可认为小球与Q接触过程中不损失机械能．小球从接触Q开始，经历时间T0第一次把弹簧压缩至最短，然后又被弹簧弹回．由于薄板Q的绝缘性能有所欠缺，使得小球每次离开弹簧的瞬间，小球的电荷量都损失一部分，而变成刚与弹簧接触时小球电荷量的
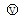（量程为6V，内阻很大，其负接线柱与B极相连，正接线柱与探针P相连），开关K．现要用图中仪器描绘两平行金属条AB间电场中的等势线．AB间的电压要求取为6V．