Question

【题目】A、B 两个半径相同的天体各有一个卫星 a、b 环绕它们做匀速圆周运动，两个卫星的 质量相等，环绕周期之比为 4：1，A、B 各自表面重力加速度之比为 4：1（忽略天体的 自转），则（ ）

A.a、b 轨迹半径之比为 4：1

B.a、b 的动能之比为 1：1

C.A、B 密度之比为 4：1

D.a、b 所受向心力之比为 1：16

Answer 1

【答案】ABC

【解析】

设天体半径为R，卫星轨道半径为r，两卫星分别绕两天体做匀速圆周运动是由万有引力提供向心力，有

解得

天体表面的重力等于万有引力，有

可得

A．由和可得轨道半径为

则a和b的轨道半径之比为

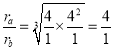
故A正确；

B．运行速度为

动能为

因卫星a、b的质量相等，A、B各自表面重力加速度之比为4：1，则可推得卫星a、b动能之比为1：1，故B正确；

C．天体AB的密度

则A、B密度之比为4：1，故C正确；

D．卫星a、b所受向心力为

向心力之比为1：4，故D错误。

故选ABC。