题目内容
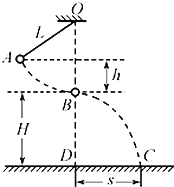
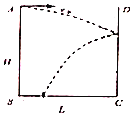
【题目】如图所示，一箱子高为H．底边长为L，一小球从一壁上沿口A垂直于箱壁以某一初速度向对面水平抛出，空气阻力不计。设小球与箱壁碰撞前后的速度大小不变，且速度方向与箱壁的夹角相等。
（1）若小球与箱壁一次碰撞后落到箱底处离C点距离为
，求小球抛出时的初速度v0；
（2）若小球正好落在箱子的B点，求初速度的可能值。
【答案】（1）
（2）
【解析】
（1）将整个过程等效为完整的平抛运动，结合水平位移和竖直位移求解初速度；（2）若小球正好落在箱子的B点，则水平位移应该是2L的整数倍，通过平抛运动公式列式求解初速度可能值。
（1）此题可以看成是无反弹的完整平抛运动，
则水平位移为：x＝
＝v0t
竖直位移为：H＝
gt2
解得：v0＝ ；
（2）若小球正好落在箱子的B点，则小球的水平位移为：x′＝2nL（n＝1.2.3……）
同理：x′＝2nL＝v′0t，H＝gt′2
解得：
（n＝1.2.3……）
练习册系列答案
相关题目
