题目内容
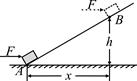
如图所示,一个小球(视为质点)从H=12 m高处,由静止开始通过光滑弧形轨道AB,进入半径R=4 m的竖直圆环,且圆环动摩擦因数处处相等,当到达环顶C时,刚好对轨道压力为零;沿CB圆弧滑下后,进入光滑弧形轨道BD,且到达高度为h的D点时的速度为零,则h之值不可能为(g取10 m/s2,所有高度均相对B点而言)( )
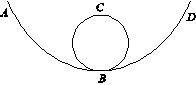

| A.12 m | B.10 m | C.8.5 m | D.7 m |
ABD
试题分析: 小球到达环顶C时,刚好对轨道压力为零,在C点,由重力充当向心力,则根据牛顿第二定律得:
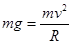 ,解得:
,解得: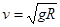 ,开始小球从H="12m" 高处,由静止开始通过光滑弧形轨道ab,因此在小球上升到顶点时,根据动能定理得:
,开始小球从H="12m" 高处,由静止开始通过光滑弧形轨道ab,因此在小球上升到顶点时,根据动能定理得: ,之后小球沿轨道下滑,由于机械能有损失,所以下滑速度比上升速度小,因此对轨道压力变小,所受摩擦力变小,所以下滑时,摩擦力做功大小小于Wf,所以全过程摩擦力做功大于Wf,小于2Wf,对全过程,用动能定理:
,之后小球沿轨道下滑,由于机械能有损失,所以下滑速度比上升速度小,因此对轨道压力变小,所受摩擦力变小,所以下滑时,摩擦力做功大小小于Wf,所以全过程摩擦力做功大于Wf,小于2Wf,对全过程,用动能定理: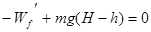
所以高度范围为8m<h<10m,故选A、B、D。

练习册系列答案
相关题目


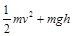
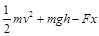



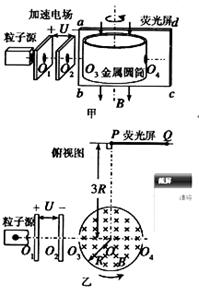
 为加速电场两极板上的小孔,
为加速电场两极板上的小孔,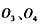 为圆筒某一直径两端的小孔,abcd为竖直荧光屏,光屏与直线
为圆筒某一直径两端的小孔,abcd为竖直荧光屏,光屏与直线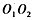 平行。开始时
平行。开始时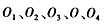 在同一水平线上。已知加速电压为U,圆简半径为R,带正电的粒子质量为m,电量为q,圈筒转轴到光屏的距离OP=3R(如图乙)。不计位子重力及粒子间相互作用。
在同一水平线上。已知加速电压为U,圆简半径为R,带正电的粒子质量为m,电量为q,圈筒转轴到光屏的距离OP=3R(如图乙)。不计位子重力及粒子间相互作用。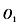 进人电场时的速度可忽略,求粒子通过圆筒的时间to
进人电场时的速度可忽略,求粒子通过圆筒的时间to (如图乙)。求粒子到达光屏时的速度大小v的范围,以及圆筒转动的角速度
(如图乙)。求粒子到达光屏时的速度大小v的范围,以及圆筒转动的角速度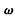 。
。