题目内容
【题目】如图所示，现有一端固定在地面上的两根长度相同竖直弹簧（K1＞K2），两个质量相同的小球分别由两弹簧的正上方高为H处自由下落，落到轻弹簧上将弹簧压缩，小球落到弹簧上将弹簧压缩的过程中获得的最大弹性势能分别是E1和E2 ， 在具有最大动能时刻的重力势能分别是EP1和EP2（以地面为重力势能的零势能），则（ ）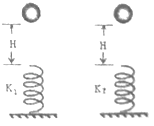
A.E1＜E2
B.E1＞E2
C.EP1=EP2
D.EP1＞EP2
【答案】A,D
【解析】解：小球压缩弹簧的过程中，受重力和支持力，在平衡位置，速度最大，动能最大，根据平衡条件，有：
kx=mg
解得：x= 
由于K1＞K2 ， 所以K1弹簧的弹力先等于重力，小球的动能最大时即K1弹簧的压缩量小，小球的位置高，可知在具有最大动能时刻的重力势能分别是EP1＞EP2 ．
由于K1＞K2 ， 弹簧K1先更难被压缩，所以到达最低点时，弹簧K1的压缩量小，小球的位置比较高，则小球减小的重力势能比较小，根据小球与弹簧的系统的机械能守恒可知，弹簧K1的弹性势能就比较小E1＜E2；所以选项AD正确，BC错误．
故选：AD
【考点精析】解答此题的关键在于理解动能定理的综合应用的相关知识，掌握应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷．
练习册系列答案
相关题目
