题目内容

（2010?北京）一物体静置在平均密度为ρ的球形天体表面的赤道上．已知万有引力常量G，若由于天体自转使物体对天体表面压力恰好为零，则天体自转周期为（　　）
分析：物体对天体压力为零，根据万有引力等于向心力可以求出周期，同时根据质量和密度关系公式即可求解周期与密度关系式．
解答：解：万有引力等于向心力
G
Mm
R2
=m(
2π
T
)2R
解得
M=
4π2R3
GT2

又由于
M=ρV=ρ（
4
3
πR3）
因而
4π2R3
GT2
=ρ（
4
3
πR3）
解得
T=
3π
Gρ

故选D．
点评：本题关键是抓住万有引力等于向心力列式求解，同时本题结果是一个有用的结论！
练习册系列答案
相关题目
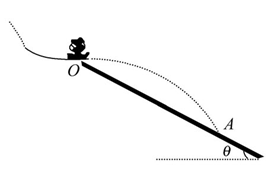
（2010?北京）如图，跳台滑雪运动员经过一段加速滑行后从O点水平飞出，经过3.0s落到斜坡上的A点．已知O点是斜坡的起点，斜坡与水平面的夹角θ=37°，运动员的质量m=50kg．不计空气阻力．（取sin37°=0.60，cos37°=0.80；g取10m/s2）求：
（1）A点与O点的距离L；
（2）运动员离开O点时的速度大小；
（3）运动员落到A点时的动能．
（2010?北京）一列横波沿x轴正向传播，a，b，c，d为介质中的沿波传播方向上四个质点的平衡位置．某时刻的波形如图1所示，此后，若经过
3
4
周期开始计时，则图2描述的是（　　）
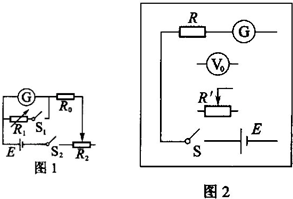（2010?北京）（1）甲同学要把一个量程为200μA的直流电流计G，改装成量范围是0～4V的直流电压表．
①她按图1所示电路、用半偏法测定电流计G的内电阻rg，其中电阻R0约为1kΩ．为使rg的测量值尽量准确，在以下器材中，电源E应选用
B
B
，电阻器R1应选用
C
C
，电阻器R2应选用
F
F
（选填器材前的字母）．
A．电源（电动势1.5V）B．电源（电动势6V）
C．电阻箱（0～999.9Ω）D．滑动变阻器（0～500Ω）
E．电位器（一种可变电阻，与滑动变阻器相当）（0～5.1kΩ）
F．电位器（0～51kΩ）
②该同学在开关断开情况下，检查电路连接无误后，将R2的阻值调至最大．后续的实验操作步骤依次是：
B
B
，
C
C
，
A
A
，
E
E
，最后记录R1的阻值并整理好器材．（请按合理的实验顺序，选填下列步骤前的字母）
A．闭合S1
B．闭合S2
C．调节R2的阻值，使电流计指针偏转到满刻度
D．调节R2的阻值，使电流计指针偏转到满刻度的一半
E．调节R1的阻值，使电流计指针偏转到满刻度的一半
F．调节R1的阻值，使电流计指针偏转到满刻度
③如果所得的R1的阻值为300.0Ω，则图1中被测电流计G的内阻rg的测量值为
300
300
Ω，该测量值
略小于
略小于
实际值（选填“略大于”、“略小于”或“等于”）．
④给电流计G
串
串
联（选填“串”或“并”）一个阻值为
19.7
19.7
kΩ的电阻，就可以将该电流计G改装为量程4V的电压表．
（2）乙同学要将另一个电流计G改装成直流电压表，但他仅借到一块标准电压表V0、一个电池组E、一个滑动变阻器R′和几个待用的阻值准确的定值电阻．
①该同学从上述具体条件出发，先将待改装的表G直接与一个定值电阻R相连接，组成一个电压表；然后用标准电压表V0校准．请你画完图2方框中的校准电路图．
②实验中，当定值电阻R选用17.0kΩ时，高整滑动变阻器R′的阻值，电压表V0的示数是4.0V时，表G的指针恰好指到满量程的五分之二；当R选用7.0kΩ时，调整R′的阻值，电压表V0的示数是2.0V，表G的指针又指到满量程的五分之二．由此可以判定，表G的内阻rg是
3.0
3.0
kΩ，满偏电流Ig是
0.50
0.50
mA．若要将表G改装为量程是15V的电压表，应配备一个
27.0
27.0
kΩ的电阻．

(2010·北京高考)如图，跳台滑雪运动员经过一段加速滑行后从Ｏ点水平飞出，经过3.0 ｓ落到斜坡上的Ａ点.已知Ｏ点是斜坡的起点，斜坡与水平面的夹角θ＝37°，运动员的质量m="50" kg.不计空气阻力.(取sin37°=0.60，cos37°=0.80；g取10 m／s2)求：

(１)A点与O点的距离；
(２)运动员离开O点时的速度大小；
(３)运动员落到A点时的动能.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网