��Ŀ����
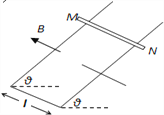
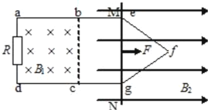
����Ŀ����ͼ��ae��dgΪ�����ƽ�С�ˮƽ���õĽ������죬��ad�˽�һ����ֵΪR�Ķ�ֵ���衣�߳�ΪL��������abcd��������һ����ֱ���µ���ǿ�ų�B1��B1��ʱ���������ef��fgΪ����������������f����Ե����ͨ��efg����һ���ȱ������Σ�������һˮƽ��ǿ�ų��У��Ÿ�Ӧǿ�ȴ�СΪB2��������MN��ֱ����ae��dg������egλ�ô�����t=0ʱ������һ����ֱ������������F����������������Ϊv������ֱ���˶�����·�ڲ����ĸ�Ӧ����ΪI����֪������������Ϊm�����費�ƣ���efg����Ķ�Ħ������Ϊ�����������ٶ�Ϊg����
��1��B1��ʱ���������ı仯�ʣ�
��2������F��ʱ��t�仯�ı���ʽ��
��3��������˶������Ҷ�f��Ĺ����У���·��Ħ������������Q��
���𰸡���1��B1��ʱ���������ı仯��Ϊ![]() ����2������F��ʱ��t�仯�ı���ʽΪ
����2������F��ʱ��t�仯�ı���ʽΪ![]() ����3��������˶������Ҷ�f��Ĺ����У���·��Ħ������������QΪ
����3��������˶������Ҷ�f��Ĺ����У���·��Ħ������������QΪ![]() ��
��
��������
��1�����ݷ����ڵ�Ÿ�Ӧ����
![]()
��ã�
![]()
��2����������
F=����mg+B2ILx��
������
![]()
��ã�
![]() ��
��![]() ����
����
��3��Ħ������ƽ����
![]()
�˷�Ħ������������Ħ������������Q
![]()
�����ã�
![]() ��
��

 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д� һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�����Ŀ����ͬ�Ľ��������䵼�����ܲ�ͬ�����ǿ����õ絼G����λ��������S����������
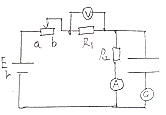
��1��Ϊ�˵õ�����ͭ���ߵĵ絼G����Щ�����йأ��ڿ���ʵ�����¶Ȳ���������£�ij��ͬѧ������ʵ�顣��ʵ�����ݻ������£�
����ֱ��d��mm�� | 1 | 2 | 3 | 2 | 2 | 2 |
���߳���l��cm�� | 10 | 10 | 10 | 20 | 30 | 40 |
�絼G��S�� | 468 | 1875 | 4219 | 937 | 625 | 468 |
���ݱ������ݿɵã��絼G��_____�����ȣ���_____�ɷ��ȣ�
��2��Ϊ�˲�����ͬ�����ĵ������ܣ�����ͬѧ����ֱ��Ϊ1mm������Ϊ10cm�IJ�ͬ�������߽����˽�һ�����������ݻ������£�
���� | ͭ | �� | �� | �� |
�絼G��S�� | 468 | 300 | 86 | 136 |
�������˵�ѹU��V�� | 1.07��10��3 | 3.33��10��3 | 0.017 | 0.015 |
�������ߵ���I��A�� | 0.5 | 1 | 1.5 | 2 |
���ݱ������ݿɵã��絼G���ѹU������I�Ĺ�ϵʽΪ��_____�����ֽ����У�����_____�ĵ���������