题目内容
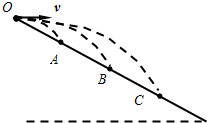 如图,质量相同的三个小球从足够长的斜面上同一点O分别以初速度v1、v2、v3水平抛出,落在斜面上的位置分别是A、B、C,已知OA=AB=BC,空气阻力不计,则( )
如图,质量相同的三个小球从足够长的斜面上同一点O分别以初速度v1、v2、v3水平抛出,落在斜面上的位置分别是A、B、C,已知OA=AB=BC,空气阻力不计,则( )分析:三个小球做平抛运动,运用运动的分解法,得出斜面的长度与初速度、运动时间的关系,再求解初速度、时间的比值.根据动能定理研究动能的增量.
解答:解:设物体的初速度为v0,O点到斜面落点的长度为L,斜面的倾角为θ.
则tanα=
=
=
,得t=
①
则有L=
=
=
,②
θ一定,则得到L∝
小球落在斜面上速度平方为v2=
+(gt)2=
(1+2tan2θ)
落到斜面时的动能为Ek=
mv2=
m
(1+2tan2θ)③
由题,OA=AB=BC,则v1:v2:v3=1:
:
由①得,飞行时间之比为t1:t2:t3=v1:v2:v3=1:
:
由③得,落到斜面时的动能之比为1:2:3.
根据动能定理得,飞行过程中动能增量△Ek=mgLsinθ=2mg
tan2θ∝
,
得飞行过程中动能增量之比为1:2:3.
故选BC
则tanα=
| y |
| x |
| ||
| v0t |
| gt |
| 2v0 |
| 2v0tanθ |
| g |
则有L=
| x |
| cosθ |
| v0t |
| cosθ |
2
| ||
| cosθ |
θ一定,则得到L∝
| v | 2 0 |
小球落在斜面上速度平方为v2=
| v | 2 0 |
| v | 2 0 |
落到斜面时的动能为Ek=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
由题,OA=AB=BC,则v1:v2:v3=1:
| 2 |
| 3 |
由①得,飞行时间之比为t1:t2:t3=v1:v2:v3=1:
| 2 |
| 3 |
由③得,落到斜面时的动能之比为1:2:3.
根据动能定理得,飞行过程中动能增量△Ek=mgLsinθ=2mg
| v | 2 0 |
| v | 2 0 |
得飞行过程中动能增量之比为1:2:3.
故选BC
点评:本题中斜面的倾角反映了位移与水平方向的夹角,关键确定两个方向的位移关系得出时间表达式.

练习册系列答案
相关题目
 (2009?西城区一模)如图为三个高度相同、倾角不同的光滑斜面.让质量相同的三个物体分别沿三个斜面由静止从顶端运动到底端.在此过程中,三个物体的( )
(2009?西城区一模)如图为三个高度相同、倾角不同的光滑斜面.让质量相同的三个物体分别沿三个斜面由静止从顶端运动到底端.在此过程中,三个物体的( )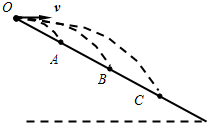
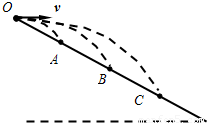 如图,质量相同的三个小球从足够长的斜面上同一点O分别以初速度v1、v2、v3水平抛出,落在斜面上的位置分别是A、B、C,已知OA=AB=BC,空气阻力不计,则( )
如图,质量相同的三个小球从足够长的斜面上同一点O分别以初速度v1、v2、v3水平抛出,落在斜面上的位置分别是A、B、C,已知OA=AB=BC,空气阻力不计,则( )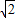 :
: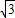
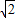 :
:
 如图,质量相同的三个小球从足够长的斜面上同一点O分别以初速度v1、v2、v3水平抛出,落在斜面上的位置分别是A、B、C,已知OA=AB=BC,空气阻力不计,则( )
如图,质量相同的三个小球从足够长的斜面上同一点O分别以初速度v1、v2、v3水平抛出,落在斜面上的位置分别是A、B、C,已知OA=AB=BC,空气阻力不计,则( )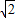 :
: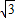
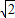 :
: