题目内容
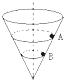一个内壁光滑的圆锥形筒的轴线垂直水平面，圆锥筒固定，有质量相等的小球A和B沿着筒的内壁在水平面内做匀速圆周运动，A的运动半径较大，则（ ）| A、球A的线速度等于球B的线速度 | B、球A的角速度等于球B的角速度 | C、球A的运动周期小于球B的运动周期 | D、球A与球B对筒壁的压力相等 |
分析：小球做匀速圆周运动，合外力提供向心力，对物体正确进行受力分析，然后根据向心力公式列方程即可分析．
解答：
解：对于任意一个小球，受力如图：将FN沿水平和竖直方向分解得：
FNcosθ=ma ①，FNsinθ=mg ②．
由于A、B两球的质量相等，两球受到的支持力相等，则小球对筒壁压力大小相等，故D正确；
由①②可得：gcotθ=a，可知两球的向心加速度大小相等．
又 a=
=ω2r=
r
所以半径大的线速度大，角速度小，周期大，与质量无关，故ABC错误．
故选：D．
解：对于任意一个小球，受力如图：将FN沿水平和竖直方向分解得：FNcosθ=ma ①，FNsinθ=mg ②．
由于A、B两球的质量相等，两球受到的支持力相等，则小球对筒壁压力大小相等，故D正确；
由①②可得：gcotθ=a，可知两球的向心加速度大小相等．
又 a=
| v2 |
| r |
| 4π2 |
| T2 |
所以半径大的线速度大，角速度小，周期大，与质量无关，故ABC错误．
故选：D．
点评：解决这类圆周运动问题的关键是对物体正确受力分析，根据向心力公式列方程进行讨论，注意各种向心加速度不同表达式形式的应用
练习册系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
相关题目
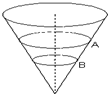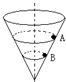一个内壁光滑的圆锥形筒的轴线垂直水平面，圆锥筒固定，有质量不相等的小球A和B沿着筒的内壁在水平面内做匀速圆周运动，A的运动半径较大，则（ ）
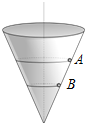一个内壁光滑的圆锥形筒的轴线垂直水平面，圆锥筒固定，有质量相同的小球A和B沿着筒的内壁在水平面内做匀速圆周运动，如图 所示，A的运动半径较大，则（ ）
一个内壁光滑的圆锥形筒的轴线垂直水平面，圆锥筒固定，有质量相等的小球A和B沿着筒的内壁在水平面内做匀速圆周运动，A的运动半径较大，则（ ）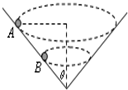
如图所示，一个内壁光滑的圆锥形筒的轴线垂直于水平面，圆锥筒固定不动，有两个质量相等的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动，则以下说法中正确的是（ ）
一个内壁光滑的圆锥形筒的轴线垂直于水平面，圆锥筒固定，有质量不相等的小球A和B沿着筒的内壁在水平面内作匀速圆周运动，如图所示，A的运动半径较大，则（ ）| A、A球的线速度必小于B球的线速度 | B、A球的角速度必小于B球的角速度 | C、A球需要的向心力等于B球需要的向心力 | D、A球对筒壁的压力可能等于B球对筒壁的压力 |