题目内容
【题目】如图所示,质量为m的物体A压在置于水平面上的劲度系数为k1的竖直轻弹簧B上.用细绳跨过定滑轮将物体A与另一根劲度系数为k2的轻弹簧C连接.当弹簧C处在水平位置且未发生形变时,其右端点位于a位置.将弹簧C的右端点沿水平方向缓慢拉到b位置时,弹簧B对物体A的拉力大小恰好等于A的重力.求: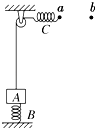
(1)当弹簧C处在水平位置且未发生形变时,弹簧B的形变大小.
(2)该过程中物体A上升的高度为多少?ab间的距离为多大.
【答案】
(1)解:当弹簧C未发生形变时弹簧B处于压缩状态,设压缩量为x0,根据平衡条件和胡克定律有:k1x0=mg,
解得:x0= ![]()
答:当弹簧C处在水平位置且未发生形变时,弹簧B的形变大小 ![]() .
.
(2)解:当弹簧C的右端点沿水平缓慢拉到b位置时,因弹簧B对物体A的拉力大小恰好等于A的重力,说明弹簧B处于伸长状态,且伸长量为:x1=x0= ![]()
所以物体A上升的高度为:h=2x0= ![]()
绳中张力为:FT=2mg
弹簧C的伸长量为:x2= ![]() =
= ![]()
ab间的距离为为:xab=h+x2=2mg( ![]() +
+ ![]() )
)
答:该过程中物体A上升的高度为 ![]() ,ab间的距离为2mg(
,ab间的距离为2mg( ![]() +
+ ![]() )
)
【解析】(1)当弹簧C处在水平位置且未发生形变时,对A进行受力分析,根据平衡求出弹簧B的弹力,再根据胡克定律求出弹簧B的形变量.(2)将弹簧C的右端点沿水平缓慢拉到b位置时,弹簧B对物体A的 拉力大小恰好等于A的重力,弹簧B处于伸长状态,根据弹力的大小求出弹簧的伸长量,从而求出距离.根据平衡求出弹簧C的拉力,再根据胡克定律求出C的形变量.

练习册系列答案
相关题目