题目内容
如图所示，水平放置的轻弹簧左端固定，小物块P（可视为质点）置于水平桌面上的A点，并与弹簧右端接触，此时弹簧处于原长。现用水平向左的推力将P缓慢地推至B点，此时弹簧的弹性势能为Ep=28J。撤去推力后，P沿桌面滑到一个上表面与桌面等高且静止在光滑水平地面上的长木板Q上，已知P、Q的质量均为m=2kg，A、B间的距离L1=4m，A距桌子边缘C的距离L2=2m，P与桌面及P与Q间的动摩擦因数都为μ=0.1，g取10m／s2，求：
（1）P刚滑到Q上时的速度大小；
（2）当Q的长度为3m时，试通过计算说明P是否会滑离Q。若不会滑离，则求出P、Q的共同速度大小；若会滑离，则求出当P滑离Q时，P和Q的速度各为多大？
（1）vC=4m/s（2）当P滑离Q时，P的速度为3m/s，Q的速度为1m/s.。
解析:应用动量守恒定律和能量守恒定律及其相关知识列方程解答。
解：（1）P从B点运动到C点的过程中，由能量守恒定律，
Ep-
mvC2=μmg(L1+L2)
解得：vC=4m/s。
（2）若P、Q最终具有共同速度v，由动量守恒定律，mvC=2mv
若P中Q上滑过的长度为s，由能量守恒定律，μmgs=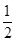mvC2 -2mv2，
解得：s=4m。
已知Q的长度L=3m小于s，则会滑离。
设P滑离Q时，它们的速度分别为vP和vQ，
由动量守恒定律，mvC=mvP+mvQ
由能量守恒定律，μmgs=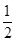mvC2 -mvP2-mvQ2
解得：vP=3m/s，vQ=1m/s。
另一组解vP=1m/s，vQ=3m/s不合题意舍弃。
因此当P滑离Q时，P的速度为3m/s，Q的速度为1m/s.
练习册系列答案
阅读快车系列答案
相关题目
如图所示，水平放置的平行金属板A、B间距为d，带电粒子的电荷量为q，质量为m，粒子以速度v从两极板中央处水平飞入两极板间，当两板上不加电压时，粒子恰从下板的边缘飞出．现给AB加上一电压，则粒子恰好从上极板边缘飞出求：（1）两极板间所加电压U；（2）金属板的长度L．
如图所示，水平放置的矩形线圈abcd的面积为S，处于竖直向下的磁感应强度为B的匀强磁场内，则穿过矩形线圈的磁通量是
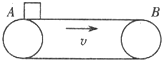如图所示，水平放置的白色的传送带以速度v=6m/s向右匀速运行，现将一小煤块轻轻地放在传送带A端，物体与传送带间的动摩擦因数μ=0.1，若A端与B端相距30m，则（g=10m/s2）（ ）| A、小煤块先作匀加速直线运动，后作匀速直线运动 | B、小煤块一直作匀加速直线运动 | C、全过程中，小煤块先受到向右的滑动摩擦力，后不受摩擦力作用 | D、全过程中，小煤块先受到向右的滑动摩擦力，后受到向右的静摩擦力作用 |
如图所示，水平放置的两块长直平行金属板a、b相距d=0.10m，a、b间的电场强度为E=5.0×105N/C，b板下方整个空间存在着磁感应强度大小为B=6.0T、方向垂直纸面向里的匀强磁场．今有一质量为m=4.8×10-25kg、电荷量为q=1.6×10?18C的带正电的粒子（不计重力），从贴近a板的左端以υ0=1.0×106m/s的初速度水平射入匀强电场，刚好从狭缝P穿过b板而垂直进入匀强磁场，最后粒子回到边界b的Q（图中未标出）处．试求
如图所示，水平放置的平行板电容器，原来AB两板不带电，B极板接地，它的极板长L=0.1m，两板间距离d=0.4×10-2m，现有一微粒质量m=2.0×10-6kg，带电量q=+1.0×10-8C，以一定初速度从两板中央平行于极板射入，由于重力作用微粒恰好能落到A板上中点O处，不反弹．忽略平行板电容器的边缘效应，取g=10m/s2．试求：